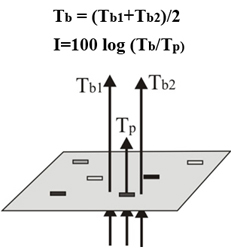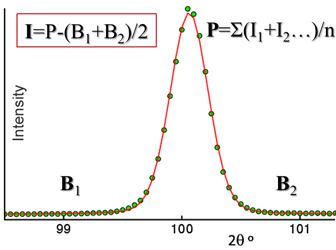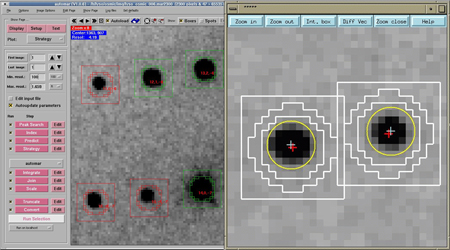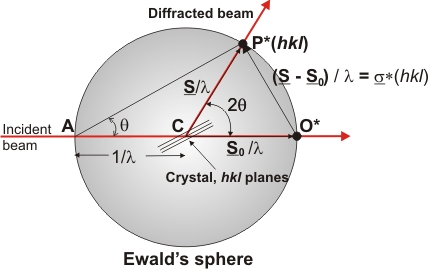

Historically speaking, detection of diffracted patterns has been carried out in different ways...
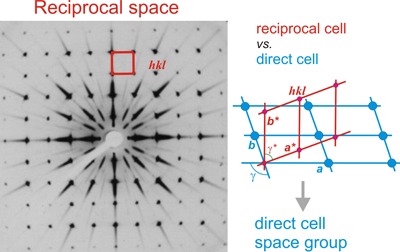
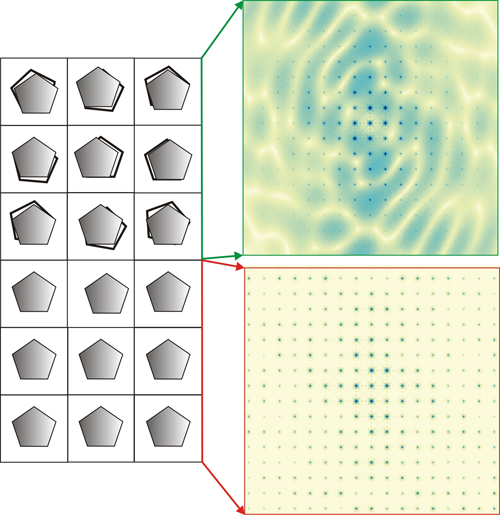
- Using photographic films, sensitive to X-rays, placed inside cameras suitable for these experiments. Diffraction cameras most frequently used were those of Weissenberg and precession. Both types of cameras were designed to generate images of any reciprocal plane. The precession diagrams (image on the left) show the arrangement of the reciprocal points with the real geometry of the lattice, but the diagrams obtained with the Weissenberg cameras provide distorted images of these planes, and therefore it is necessary to know how to interpret the geometric distortion that contain the Weissenberg diagrams for its correct interpretation.


Photographic films showing part of a diffraction pattern
Precession camera (left) and Weissenberg camera (right)
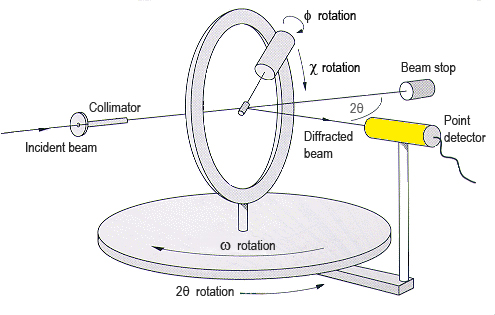
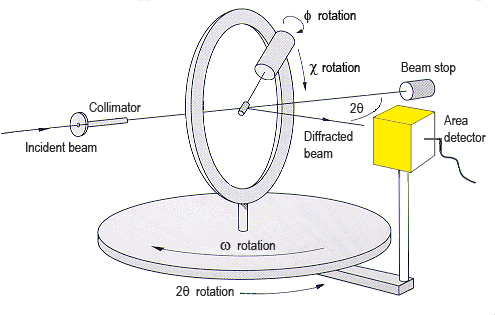
- Using specific point detectors placed in the path of each diffracted beam, although orienting the crystal in such a way that the diffracted beam occurs on the equatorial plane of the Ewald sphere. This process is achieved using four-circle goniometers.