5.
Dispersión
y difracción
En
el
contexto de este capítulo Vd será invitado
también a visitar estos apartados...
La radiación
electromagnética
(como por ejemplo la luz visible) puede interaccionar consigo misma y
con la materia, dando lugar a multitud de
fenómenos como la reflexión,
la refracción,
la dispersión,
la polarización
...
Derecha: Polarización
de la luz a su paso por un polarizador. Dependiendo del giro del
polarizador, se filtra uno de los componentes de la luz no polarizada
que incide desde la derecha de la imagen
Animaciones
originalmente tomadas de physics-animations.com
Pues bien, la
difracción
(de los rayos X) es el fenómeno físico a
través del
cual se manifiesta la interacción
fundamental de los rayos X con los cristales (materia
ordenada). Sin
embargo, para poder describir el fenómeno,
es recomendable introducir previamente algunos modelos
físicos que, como todos los modelos, no explican totalmente
la realidad, pues
suponen una idealización de la misma, pero nos sirven para
comprender el fenómeno.
Sobre ondas
Una onda, es decir,
un fenómeno
ondulatorio, corresponde a
la propagación en el
espacio y en el tiempo de una perturbación oscilatoria, es
decir, un fenómeno regularmente repetido.
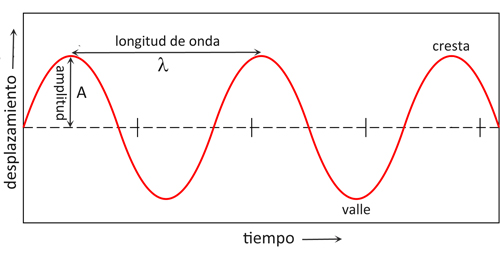
Las ondas normalmente se
representan gráficamente por una
función de tipo sinusoide (tal como se muestra en la figura
de arriba), en la que
podemos definir algunos parámetros generales que la definen.
Propagación
ondulatoria transversal de movimientos vibratorios longitudinales y
circulares.
Animaciones
originalmente tomadas de physics-animations.com
Una perturbación
ondulatoria (una onda) se propaga a una cierta velocidad
(v)
y se modela satisfaciendo la llamada ecuación de ondas,
escalar o vectorial, dependiendo de la naturaleza de la
perturbación.
Las soluciones de esta ecuación son, en general,
combinaciones de términos
trigonométricos que vienen caracterizados, cada
uno, por una
amplitud
(A),
que mide el valor extremo (máximo o mínimo)
respecto de una situación
de equilibrio de la perturbación, y una fase
Φ:
Φ =
2π(K.r
- ν.t
+ α)
La intensidad
de la perturbación en un punto es proporcional al cuadrado
del valor de la perturbación; y si ésta
está expresada como
exponenciales complejas, esto equivale al producto de la
perturbación
por su complejo conjugado. La intensidad
es una medida del flujo de energía por unidad de tiempo y
por unidad
de área del frente de onda, plano o esférico,
dependiendo del tipo de onda.
La
perturbación queda periódica, es decir, se repite
exactamente en el tiempo (con
periodo T)
y en el
espacio (con periodo λ,
la longitud de onda), de forma que λ
= ν.T,
o sea, λ.ν=
v.
En la expresión de la
fase (Φ),
K
es el vector
de ondas que da el
sentido de avance de la perturbación, el
rayo,
y se considera de módulo 1/λ.
Es pues el número de repeticiones por unidad de longitud.
ν es
la frecuencia
(la inversa del periodo), es decir, el número de
repeticiones, o ciclos de repetición
de una situación, por unidad de tiempo. Se llama
pulsación
a: 2π.ν,
y mide las repeticiones por cada radián del ciclo.
En
el espectro
electromagnético (es decir, en la
distribución de las longitudes de onda
electromagnéticas), los rayos X duros (de alta
energía), se sitúan alrededor de una longitud de
onda de 1 Angstrom en el vacío (para el Cu
es, en media, de 1.5418,
y para el Mo
0.7107 Angstrom), mientras que la luz
visible se sitúa en el rango que va desde 4000
a 7000 Angstrom.
t
y
r
son, respectivamente, el tiempo y el vector de posición del
punto en donde se considera la perturbación, y α
es el defase original relativo a las otras componentes.
Se habla de ondas en
fase si la diferencia de fases entre estas
componentes es un
múltiplo entero de 2π,
y
en
oposición de fase si es
múltiplo impar de π.
Por facilidad matemática, para llevar la cuenta de las
relaciones entre
las fases de las componentes de la onda, a estos términos se
les
suele expresar en notación exponencial, exponenciales
imaginarias donde la unidad i,
imaginario puro, expresa un defase de
+π/2.
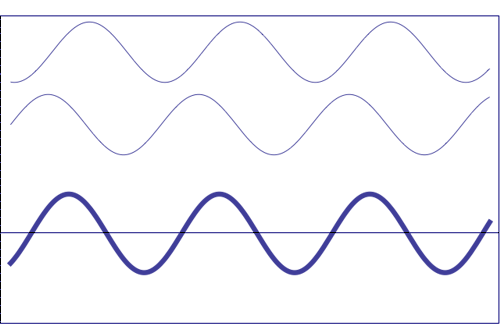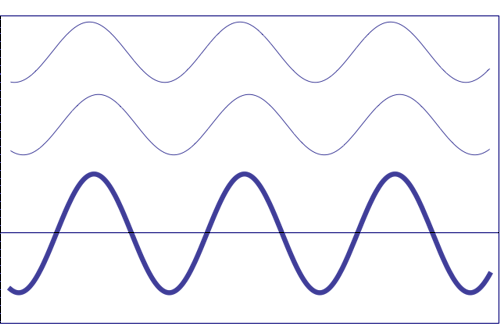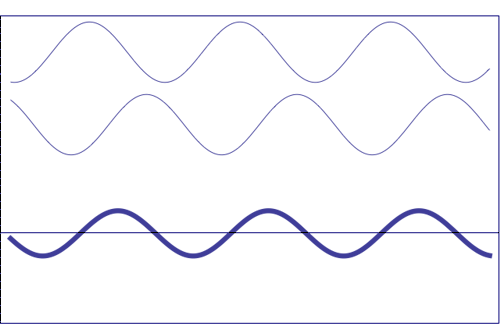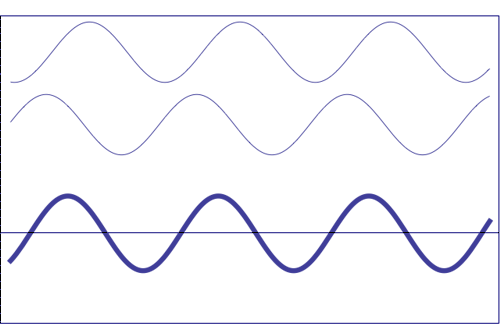
Posibles estados
de interferencia de las dos ondas de la parte superior, con la
misma amplitud y frecuencia. La onda de trazo grueso
(representada en
la parte inferior) muestra la resultante de la interferencia, que llega
a tener amplitud máxima cuando las ondas que se
componen se solapan (son
totalmente coincidentes), es decir, que están en fase. La interferencia totalmente
destructiva (amplitud resultante nula) se
obtiene cuando los
máximos de una de las componentes son
coincidentes con los mínimos de la otra, es decir,
cuando las dos ondas están
en oposición de fase.
Animación
tomada de The
Pennsylvania State University
Cuánticamente,
la energía que caracteriza la radiación es
proporcional a
la frecuencia, y es ésta la que es independiente del medio y
caracteriza
que la radiación sea monocromática. La λ
correspondiente
dependerá de la velocidad que alcance en el medio, es decir,
depende
de la estructura y composición de éste.
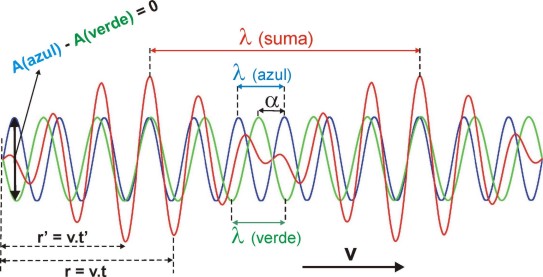
Perturbación
ondulatoria correspondiente a la combinación de dos ondas
elementales
(azul
y verde)
de longitudes de onda próximas (λ, λ),
con la misma amplitud (A,
A)
y con defase respectivo α.
La
perturbación avanza de izquierda a derecha con velocidad v. La suma de ambas
ondas
individuales produce una perturbación resultante que se
representa en color rojo
(λ).
Las
soluciones de la ecuación
de ondas modelo, cuya amplitud no depende
inversamente de la distancia del origen al punto de
observación, se
llaman ondas planas, pues en un tiempo dado todos los puntos del plano
K.r
=
constante
tienen la misma fase, el plano es perpendicular al vector de
propagación
K,
y estos planos de fase constante se propagan con velocidad v.
v
es, pues, la velocidad de fase. Para una perturbación
resultante
de varias componentes, el pulso viaja con la llamada velocidad
de grupo. y el lector interesado puede consultar la
simulación que se ofrece a través de este enlace.
En las soluciones de
la
ecuación en las que la amplitud depende inversamente de la
distancia,
los planos se convierten en esferas y se obtienen ondas
esféricas, que si la distancia de observación es
muy grande, pueden
asimilarse a ondas planas en el punto de observación.
El principio de
superposición
indica que la perturbación en un tiempo y en un punto,
debido a una serie de fuentes coherentes
(que no varian las relaciones de fase entre ellas), es la suma de las
perturbaciones individuales en ese tiempo y en ese punto, teniendo en
cuenta las fases
individuales (proceso llamado de interferencia),
como en la figura de arriba.
Si no hay
coherencia, las relaciones de fase varían con el tiempo, de
forma no
regular, y para obtener la intensidad de la perturbación
total, basta
con sumar intensidades (ver figura de abajo):
La perturbación total,
unión de dos fuentes no
coherentes, es
la
simple suma de las intensidades individuales
Para modelizar la
composición
de ondas trigonométricas simples de tipo seno o coseno, o
bien en su forma exponencial imaginaria, se usa la
representación de
Fresnel. En ella se supone cada onda oscilando sobre el eje X
como
proyección del movimiento circular de un vector de radio
igual a la amplitud
correspondiente y de velocidad angular igual a la
pulsación ω
de la onda en cuestión. La resultante total se
podrá hacer componiendo los vectores y proyectando la
resultante sobre el mismo eje
X:
Representación
de Fresnel (o de Argand) en la que se modeliza la
composición de
diferentes (fj)
perturbaciones
ondulatorias.
|F|
es
la amplitud de la perturbación resultante y Φ
la fase de ella.
Interacción
de los rayos X con la materia
Los rayos X interaccionan con la materia a través de los
electrones que la forman y que se están moviendo a
velocidades mucho
menores que la de la luz. Cuando la radiación
electromagnética X
alcanza un electrón cargado éste se convierte en
fuente de radiación electromagnética secundaria
dispersada.
Según
la longitud de onda y de las relaciones de fase de esta
radiación
dispersada, nos podemos referir a procesos
elásticos,
o inelásticos
(dispersión
Compton),
dependiendo de que no cambie, o cambie, la longitud de onda, y de coherencia
o incoherencia
según que las relaciones de fase se mantengan en el tiempo y
en
el espacio, o no.
Los
intercambios de energía y momento que se producen pueden
incluso
dar lugar a la expulsión de un electrón fuera del
átomo, seguido de la ocupación del nivel de este
electrón por electrones de niveles superiores.
Todos
estos tipos de interacciones dan lugar a diferentes procesos en el
material
como pueden ser: refracción,
absorción,
fluorescencia,
dispersión
Rayleigh,
dispersión
Compton, polarización,
difracción,
reflexión,
...
El
índice de refracción
de todos los materiales, con relación a los rayos X, es
próximo
a la unidad, por lo que el fenómeno de la
refracción de
rayos
X es despreciable, y provoca que no se puedan fabricar lentes para
ellos.
Por lo tanto, el proceso de formación de
imágenes, como
en
el caso de la luz visible, no se puede llevar a cabo con los rayos X.
La
absorción
se produce por la atenuación del haz transmitido al perder
energía
por todo tipo de interacciones, fundamentalmente las
térmicas,
la
fluorescencia, las dispersiones inelásticas, la
formación
de radicales libres y otras modificaciones químicas (que
pueden
llegar a dar lugar a la degradación del material). La
disminución
de intensidad sigue un modelo exponencial con la distancia atravesada
del
material y un coeficiente (coeficiente de absorción lineal)
que
depende de la densidad y composición del material.
Los
procesos de fluorescencia,
en los que un electrón es arrancado de un nivel
energético
del átomo, suministran información sobre la
composición
química del material. Debido a la expulsión de
electrones
de los diferentes niveles, se producen discontinuidades bruscas en la
absorción
contínua de la radiación por el material, lo que
permite
análisis local alrededor de un átomo (EXAFS).
En
el efecto
Compton,
la interacción es inelástica y la
radiación sale
con
menor energía. Este fenómeno siempre
está presente
en la interacción de los rayos X con la materia, pero por su
baja
intensidad, su incoherencia y por afectar a todas las direcciones,
contribuye
sólo a la radiación de fondo producida en la
interacción.
Por
dispersión
nos vamos a referir aquí a los cambios de
dirección que
sufre
la radiación incidente, y NO al caso de la
separación de
radiación en componentes según la longitud de
onda.
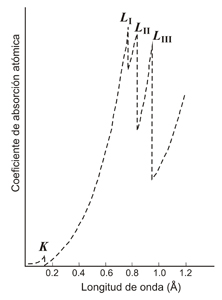
Izquierda: Variación
de la absorción de un material según la longitud
de onda
de la radiación incidente
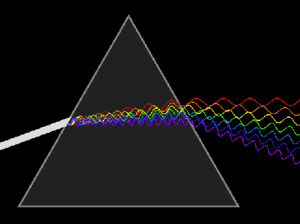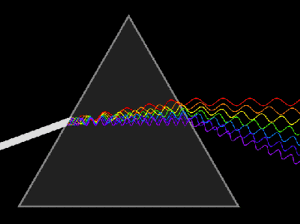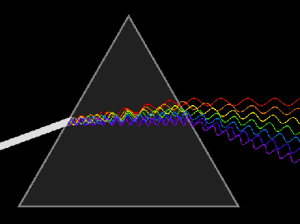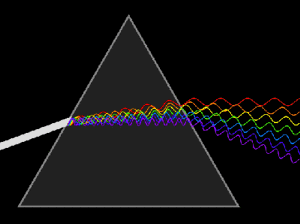
Derecha: Descomposición
de una luz blanca en sus diferentes
componentes,
casi monocromáticas
Dispersión
elástica por un electrón
Modelo
de interacción de un frente de ondas X con un
electrón
aislado, el cual se convierte en un centro emisor de ondas X de tipo
esférico.
Modelo
de interacción
de un frente de ondas X con dos electrones, que se convierten en
centros emisores de radiación X, tal como ocurre en la
imagen de
la izquierda. Sin embargo, las ondas emitidas por cada uno de
éstos interaccionan entre sí, generando
zonas de
interferencias constructivas y destructuvas.
Animaciones
originalmente tomadas de physics-animations.com
Ie(Ks)
=
I0 [e4 / R02 m2 c4] [( 1 + cos2 2θ)
/ 2]
Modelo
de dispersión de Thomson
Ks
es el vector de
dispersión, R0 es
la distancia al punto de observación, 2θ
es el ángulo
entre la dirección incidente y la
dirección
en donde se observa la dispersión; e
y m
son la carga y la masa del
electrón, respectivamente, y c
es la velocidad de propagación de la radiación en
el
vacío.
Este
es el modelo de Joseph
John Thomson (1856-1940), enunciado en 1906, sobre
la onda esférica dispersada
elásticamente por
un
electrón libre, análogo a la dispersión
Rayleigh con
luz visible. La onda es
elástica,
coherente y esférica. El factor de masa en el denominador
justifica
que se desprecie la dispersión nuclear.
La
ligadura del electrón al atómo no se considera en
el
modelo,
es decir, se supone que las frecuencias propias de vibración
del
electrón son mucho menores que la de la radiación
incidente.
En esta dispersión normal (frente al caso anómalo
en el
que
las frecuencias mencionadas son comparables) la onda dispersada
está
justo en oposición de fase con la incidente.
El
segundo factor entre corchetes, que depende del
ángulo θ,
se
conoce como factor
de
polarización,
pues la radiación dispersada se polariza
parcialmente, y por lo tanto crea una anisotropía
con relación a la dirección de
vibración del
electrón,
y una reducción de la intensidad dispersada,
según la
dirección.
La intensidad dispersada tiene simetría de
rotación
alrededor
de la dirección incidente. La proporcionalidad inversa con
la
distancia
al cuadrado, al ser la onda dispersada esférica, hace que la
energía
por unidad de ángulo
sólido
sea constante.
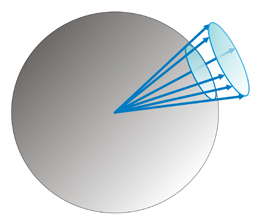
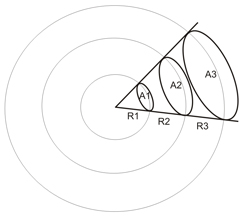
Se
conoce como ángulo sólido el cociente constante
entre las
áreas de la intersección de una secuencia
cualquiera de
esferas
con un cono y el cuadrado de los radios de las esferas.
A1/R12
= A2/R22 = A3/R32 =
... = ángulo
sólido, expresado
en estereo-radianes
El
factor de defase geométrico
Con
relación a los fenómenos de interferencia y
difracción,
es importante considerar la relación de fase entre dos ondas
que
resulta de la diferencia geométrica de caminos recorridos.
Este
defase repercute en la componente α
de la fase de la perturbación resultante total:
Φ = 2π(K0.r - ν.t
+ α)
de
forma que:
α
=
2π
(Ks -
K0)
rij
+ α '
donde K0
es
el vector de onda incidente, Ks
es
el vector de onda en la dirección de propagación
y rij
es
el vector entre los dos centros de propagación que producen
el
defase.
Si
tenemos varios centros de propagación y relacionamos sus
defases
respecto de un origen común, considerando los vectores de
posición rj
el
defase correspondiente a un centro podría expresarse (usando
vectores
unitarios en las direcciones de propagación, con λK
= s)
como:
αj
=
2
π
[(
s
-
s0)
/
λ]
rj
+
α
'
es decir, que todos
los
puntos rj
en los que el producto (s - s0) rj sea
constante, tienen la misma fase, que vendrá dada por:
Dispersión
por un átomo
Un átomo se
considera
como un conjunto de Z
electrones (su número
atómico), por
lo tanto, se esperaría que dispersara Z
veces lo que un
electrón.
Pero las distancias entre los electrones de un átomo son del
orden
de la longitud de onda de los rayos X, por lo que aparecen relaciones
de
fase entre las ondas dispersadas por cada electrón, dando
lugar
a efectos de interferencia
parcialmente
destructiva.
Así que un átomo
sólo
dispersa Z
veces
en la dirección de los rayos X incidentes, mientras que
decrece
a medida que aumenta θ,
y cuanto más difusa sea la nube de la
distribución
electrónica
alrededor del núcleo, mayor será la
reducción.
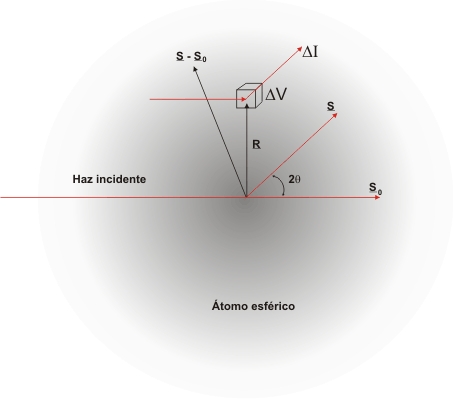Relaciones
de fase entre los electrones de un átomo
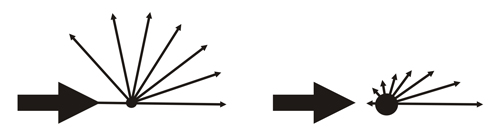Esquema que muestra la
variación de la amplitud dispersada
por un electrón
sin tener en cuenta la polarización (izquierda) y un
átomo
(derecha). La amplitud dispersada (intensidad) por un átomo
decrece a
medida que aumenta el ángulo de
dispersión.
La
intensidad de los rayos X dispersados por los electrones de un
átomo disminuye con el aumento del ángulo de
dispersión
Esquema
tomado de School of
Crystallography (Birkbeck College, Univ. of London)
Llamamos factor
atómico de dispersión (factor de "scattering")
a la razón entre la amplitud dispersada por un
átomo y la de un electrón aislado. Como la
velocidad de los electrones en el átomo
es mucho mayor que la variación del vector
eléctrico de
la onda, la radiación sólo "ve" una nube
electrónica media, que viene caracterizada por la densidad
electrónica de carga
ρ(r).
Si esta distribución se considera esféricamente
simétrica,
sólo depende de la distancia al núcleo, de forma
que, con
H
= 2 sen θ
/ λ
(que
es el módulo del vector de dispersión H
= Ks- K0
= (s
- s0) / λ):
f(H)
= 4π∫(0
→ ∞) r2 ρ(r)
(sen H
r
/ H
r)
dr
Así, el factor
atómico
de dispersión viene a representar un número de
electrones (el número efectivo de electrones en un tipo
concreto de
átomo) que dispersan en fase en esa dirección, de
forma que
a θ
=
0,
f(0)
= Z. La hipótesis de isotropía, es
decir, que este factor atómico
no depende de la dirección de H,
no
resulta muy adecuada para momentos de transición en los que
hay involucrados orbitales d
ó f,
ni para los electrones de valencia.
Por cálculos
mecanocuánticos
se obtienen los valores del factor de dispersión para cada
átomo,
y se obtienen estimaciones analíticas del tipo:
f(H) = Σ(1 → 4)
ai
exp
[ -bi
H2 ] + c
Izquierda: Factores
atómicos de dispersión calculados para iones con
el mismo
número de electrones que el Ne. Se puede
observar que el O--
tiene la nube electrónica más difusa que el Si 4+,
y por tanto, su decaimiento es más rápido
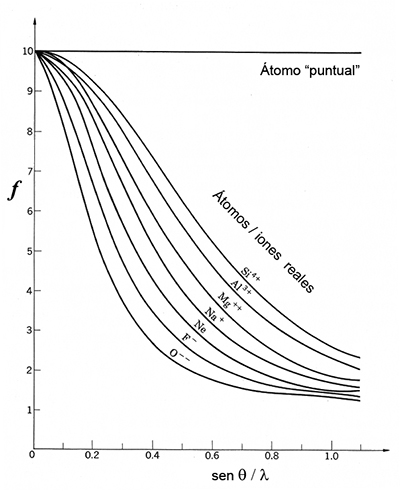
Derecha: Factores
atómicos de dispersión calculados para
átomos y iones
con diferente número de electrones. Obsérvese que
el único
electrón del hidrógeno (H) apenas
dispersa en
comparación
con los otros elementos, sobre todo a medida que aumenta Θ. El
hidrógeno es, pues, dificil de "ver" en el resultado
total de la dispersión de rayos X.
Cuando
la frecuencia de la radiación incidente es
próxima a la de
vibración natural del electrón ligado al
átomo, hay
que introducir correcciones (Δ)
debido
al defase que se produce entre las ondas elementales dispersadas por
los
electrones del átomo, cuya vibración debida al
campo incidente queda afectada por la ligadura. Así que:
f
(H) = f
0
+ Δ'
f + i Δ''
f
que también suele escribirse
como::
f(H) = f0
+ f ' +
i f ''
en donde
f0
es el factor atómico de dispersión sin ligadura,
anteriormente
definido, y la
i
es
la unidad imaginaria que viene a dar cuenta del defase de una
corrección
respecto de otra. Esta situación se produce para
átomos de
alto número atómico, es decir, pesados, o con un
número
atómico próximo (pero inferior) al del
ánodo.
Estas
correcciones al factor atómico de dispersión, que
se verán con más detalle en otro apartado,
dependen débilmente del
ángulo
θ,
por lo que el efecto anómalo se aprecia relativamente
más en valores altos de este ángulo; pero en esa
zona angular es
dónde los
haces difractados tienen menor intensidad, debido al efecto
térmico
(ver más abajo).
[Estas
correcciones nos permiten distinguir la quiralidad
(Bijvoet, 1951) de los cristales y además nos proporcionan
un método
para poder resolver las estructuras de las
moléculas (SAD,
MAD)
].
Debido a los movimientos de vibración térmica de
los
átomos dentro del material, el volumen efectivo del
átomo se amplia, lo
cual da lugar a una disminución exponencial del poder de
dispersión y está caracterizado por el
coeficiente
B
(inicialmente isotrópico) del factor exponencial de
Debye-Waller
(1913, 1923):
f(H) exp
[ -Biso sen2θ
/ λ2
]
B
es
8π2<u2>,
siendo
<u2>
la amplitud cuadrática media de vibración
térmica según
la dirección de H.
En
el modelo isotrópico de vibración, se considera
que es igual en todas direcciones, y lo más frecuente es
que B
venga a valer entre 3 y 6 Angstroms2
en cristales de compuestos orgánicos bien formados. En el
modelo anisotrópico la vibración se considera que
sigue
un modelo elipsoidal. En la práctica estos
parámetros térmicos
pueden no reflejar
únicamente la vibración, pues se ven afectados
por otros factores como desorden estático,
absorción, factores de dispersión asignados
incorrectamente, etc.
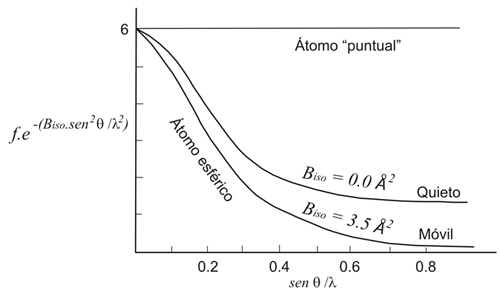Disminución del factor
atómico de dispersión debido al movimiento
térmico
Si el navegador usado se lo
permite, el lector interesado puede
igualmente consultar este "applet" de Steffen Weber
que se abrirá en una nueva ventana y que demuestra la
disminución del factor
de dispersión atómica
de un átomo cuando aumenta la temperatura, es decir, su
estado
de vibración térmica. Escriba en la columna de la
izquierda el número atómico de un
átomo (por
ejemplo 80 para el mercurio), y el mismo número en la
casilla inferior. Active el recuadro marcado con la palabra "Execute".
Observe
el decrecimiento del factor de dispersión como consecuencia
de la temperatura seleccionada. Modifique ahora la temperatura a un
valor
superior, por ejemplo 2, y vuelva a seleccionar la casilla marcada con
"Execute".
Dispersión
por un agregado de átomos
Los
rayos X dispersados por varios átomos de un material,
originan radiación en todas direcciones,
produciéndose interferencias debido a los
defases coherentes inducidos por los vectores interatómicos
que
fijan la posición relativa de los átomos. En una
molécula
o en un agregado de átomos, este efecto se conoce como
efecto de
interferencia
interna,
mientras que nos referiremos como efecto de interferencia
externa al que se produce entre moléculas o
entre agregados. Los
diagramas de dispersión reflejan la intensidad relativa de
cada uno de
estos efectos:
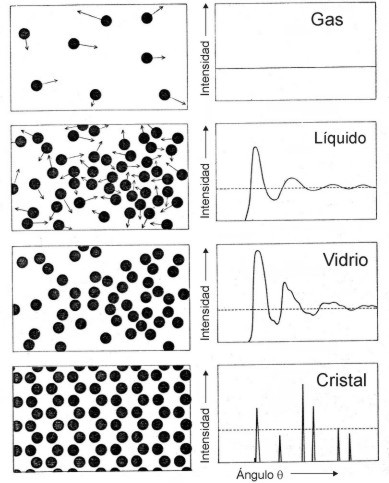
Diagramas
de dispersión de diferentes estados de un material
monoatómico. En
la representación de la intensidad se ha eliminado la
contribución
del fondo.Las
figuras representan fundamentalmente el efecto de interferencia
externo, mientras que el interno, que en este caso es debido
a un
sólo átomo, viene simplemente reflejado por la
intensidad relativa de los máximos.Obsérvese
cómo el movimiento térmico en el
líquido suaviza y disminuye el perfil de
dispersión presente en el vidrio. En
el cristal, donde las relaciones de fase son fijas y repetitivas, el
perfil
de dispersión se convierte en picos definidos donde los
otros diagramas
presentan picos anchos y contínuos. En este caso, el efecto
total
se conoce como difracción. Es
de notar cómo el fenómeno de la
dispersión refleja el "orden interno de la muestra", esto es
las correlaciones de
posición entre los átomos.
En el caso de gases
monoatómicos,
y en términos de la intensidad dispersada por un
electrón, los efectos de interferencia debidos a las
diferencias de fase entre
los
átomos m
y n,
dan lugar
a:
I(H)
= Ie(H) ΣmΣn
fm(H) fn(H) exp
[2πi
(s - s0)
rm,n
/ λ]
lo cual, cuando se
promedia
en el tiempo que dura el experimento y en todas las direcciones k
del espacio, da lugar a la fórmula de Debye:
<I
(H)>
= I
e(H) ΣmΣn
f
m(H) f
n(H) [ sen 2π|
H|
|r
m,n|
/
2π|
H|
|r
m,n|
]
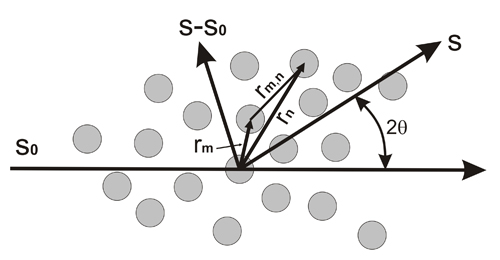Geometría
de la dispersión producida por un agregado
monoatómico
En
el caso de líquidos monoatómicos, aparecen
efectos de orden
a corta distancia, esto es, de correlación entre posiciones.
Si
la densidad de átomos por unidad de volumen, a distancia r
de cualquier átomo, con simetría
esférica es (en promedio)
ρ(r),
entonces a 4π r2ρ(r)
se le denomina función de distribución radial, y
la fórmula
de Debye
queda:
<I(H)>
= Ie(H) N f2(H)
[ 1
+ ∫(0 → ∞)
4πr2ρ(r)
sen
(2π|H|
|r|) / 2π|H|
|r|
dr ]
Todas
estas relaciones permiten el análisis de la
dispersión de rayos X en muestras amorfas,
vítreas, líquidas y gaseosas.
Con independencia de la posible
complejidad con la que se ha
presentado el fenómeno de la dispersión de los
rayos X, lo más importante es que el
lector recuerde tan sólo algunas ideas simples que se
expresan a continuación (algunas de las figuras siguientes
se han tomado de la conferencia
divulgativa de Stephen Curry)...
- Los rayos X son
dispersados por los electrones contenidos en los átomos, y
esta dispersión, que se realiza en forma de ondas en todas
las
direcciones del espacio, tiene diferentes intensidades (amplitudes),
dependiendo del número de electrones (densidad
electrónica) que están contribuyendo a esas
ondas...
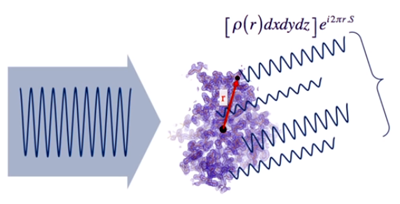
- Tomando como
origen un
punto del conjunto atómico, y considerando una determinada
dirección de
dispersión, cada una de las ondas dispersadas en esa misma
dirección se puede representar por una función
matemática (representada en esta figura), cuya amplitud
depende
de la densidad electrónica ρ(r)
existente el punto en donde se origina, siendo S
una magnitud que depende del ángulo en el que ocurre la
dispersión.
- La onda total
dispersada en cada una de las direcciones es la suma de
todas las ondas individuales que dispersan en esa misma
dirección, f(S),
y su intensidad (amplitud) dependerá de las relaciones de
fase entre cada una de las ondas, lo cual es dependiente de r
(las distancias entre los puntos en donde se originan). Y esto
ocurrirá para todas y cada una de las direcciones del
espacio...
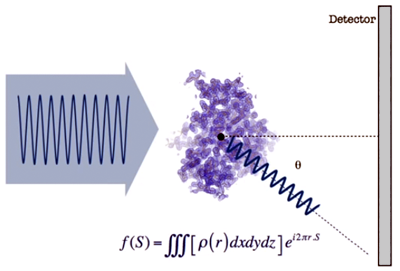
- Si colocamos un
detector
(como por ejemplo una placa fotográfica) para observar las
ondas
dispersadas, f(S),
obtendremos un conjunto de zonas de claroscuros, tal como se muestra en
la imagen de abajo...
- Este "mapa" de
ondas dispersadas (con su forma e intensidad) contiene información sobre la
distribución de los átomos que lo han originado. Matemáticamente, este mapa
se representa por la función f(S), que
es la transformada
de Fourier de la distribución de
átomos que dispersan los rayos X, es decir, de la
función de densidad electrónica.
- Más
adelante veremos que cuando los conjuntos
de átomos dispersores se agrupan de un modo ordenado, es
decir, en
forma de un cristal, éste se comporta como un amplificador
muy eficaz de la dispersión...
- En estas
circunstancias, los
efectos de la dispersión se concentran en determinadas
zonas,
muy definidas y regularmente distribuidas, efecto que conocemos como
difracción... La difracción, como efecto
amplificado de la dispersión, nos
permite obtener una información
mucho
más rica sobre
la distribución electrónica que la
origina, es decir
sobre la estructura interna de los cristales...
Dispersión
por una red monoatómica: difracción
Cuando
el agregado de átomos está estructurado
según una
red periódica tridimensional, de forma que los
átomos
constituyen nudos de esta red, las relaciones geométricas
precisas entre
los átomos del agregado dan lugar a diferencias de fase muy
particulares. Se producen composiciones cooperativas entre las ondas
dispersadas y la
muestra actúa como una red de difracción de tres
dimensiones.
En estas condiciones, los efectos de interferencia externa producen
efectos
de dispersión estructurados en picos de intensidad
máxima
y que pueden ser definidos según otra red,
recíproca
de la red directa anterior,
produciéndose unas pautas o diseños
típicos, como el que se produce cuando se observa un farol a
través de un paraguas o un visillo.
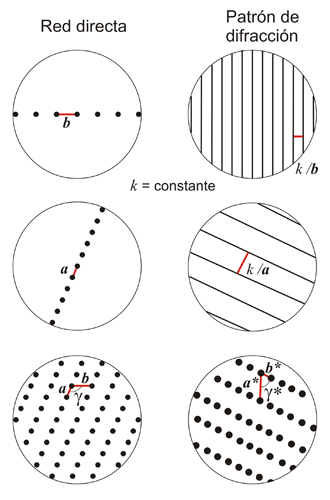
Esquema
de diagramas de difracción de distribuciones puntuales de
una y
dos dimensiones. Los parámetros de repetición en
el diagrama de difracción (espacio recíproco)
llevan el
superíndice *
y k
es un factor de escala que depende del
experimento. Todos los puntos del diagrama de difracción
tienen la misma intensidad,
pues se supone que la longitud de onda utilizada es mayor que los
puntos
de la red directa (ver más arriba el apartado de
dispersión por un átomo).
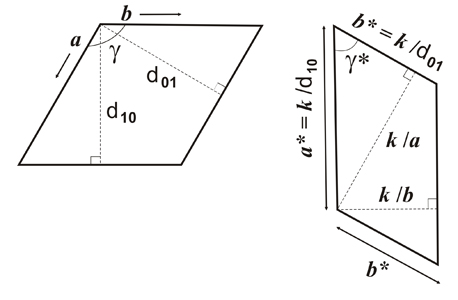
Relaciones
entre las redes bidimensionales de repetición directa
(izquierda)
y recíproca (derecha). Los parámetros de
repetición
en el espacio recíproco llevan el superíndice *
y k
es un factor de escala que depende del experimento.
d10
y d01
son los llamados espaciados de la red directa. Obsérvese que
aquí
sólo se ha representado lo que se llama una celdilla unidad
directa
y otra recíproca, correspondientes a los diagramas de
difracción
de la figura adyacente. Ver red directa y
red recíproca.
Estructurado
en red, cualquier átomo está definido por un
vector, referido a un origen común:
R
j,m1,m2,m3
= m1 a
+ m2 b
+ m3 c
en
donde Rj
da
la posición del nudo j
de
la red, m1,
m2,
m3,
son números enteros y a,
b
y c
son los vectores base que definen la red. Según esto, la
intensidad dispersada por el material sería:
I(H)
= Ie(H) Σm1Σm'1Σm2Σm'2Σm3Σm'3
fj(H)
fj'(H)
exp [2πi
(s - s0)
rm,m'
/ λ]
en
donde:
rm,m'
= Rm1,m2,m3 - Rm'1,m'2,m'3
=
(m1-m'1)
a
+ (m2 - m'2) b
+ (m3 - m'3) c
Calculando
esta suma séxtuple, se tiene:
I(H)
= Ie(H)
[ [ sen2 π(s
- s0)
M1 a
/ λ ]
/ [sen2 π(s
- s0)
a
/ λ ] ]
.
[
[ sen2 π(s
- s0)
M2 b
/ λ
]
/ [sen2 π(s
- s0)
b
/ λ ] ]
.
[ [ sen2 π(s
- s0)
M3 c
/ λ ]
/ [sen2 π(s
- s0)
c
/ λ ] ]
= I
e(H)
I
L(H)
En
esta expresión, M1,
M2,
M3
representan el número de celdillas unidad que forman el
cristal
a lo largo de las direcciones
a,
b
y c,
respectivamente,
de forma que en la muestra habría un total de M
=
M1.M2.M3
celdillas
unidad, y que en la realidad vienen a ser del orden de 1015
celdillas unidad en una muestra cristalina de 0.5 mm de espesor medio.
IL(H),
es el factor de interferencia externo debido a la estructura
monoatómica
en red. Está formado por productos del tipo (sen2
Cx) / sen2
x ,
siendo C
un
número muy grande. Esta función es
prácticamente
cero
para todo valor de x,
excepto
en los puntos en los que x
sea
un múltiplo entero de π,
en
los que toma un valor máximo de C2.
El valor total sólo será máximo cuando
los tres
productos
sean a la vez distintos de cero, donde adquirirá el valor de
M2.
Es
decir, el diagrama de difracción de la red directa de
partida es
otra red que sólo toma valor distinto de cero en los nudos y
que,
debido al factor Ie(H),
varía de un punto a otro.
Debido
al tamaño finito de las muestras, las pequeñas
diferencias
cromáticas de la radiación incidente, el mosaico
de
la muestra, ..., los máximos presentan ensanchamiento y
variaciones
de intensidad a su alrededor. Por tanto, en las condiciones
experimentales
de recogida, se necesita una pequeña oscilación
de la
muestra
alrededor de la posición de máximo (rocking)
para integrar estos efectos y recoger la energía total
dispersada.
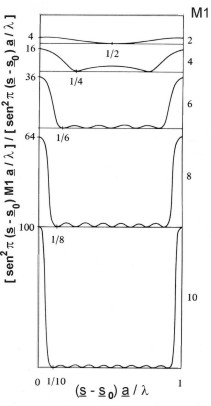
Representación
de uno de los productos que forman la función IL(H) entre
dos máximos consecutivos.
Obsérvese
el paso de la dispersión a la difracción, es
decir, a
picos
muy agudos, a medida que aumenta el número de celdillas M1.
Los
máximos son proporcionales a M12
y el
primer
mínimo va apareciendo más cercano al
máximo a
medida
que aumenta M1.
Difracción
por un cristal
Cuando
el material no está estructurado en red
monoatómica, sino
que la red está formada por un conjunto de átomos
de
igual
o de distinto tipo, la posición de cada átomo
respecto de
un origen común vendrá dado por:
R
j,m1,m2,m3
=
m1 a
+ m2 b
+ m3 c
+ rj
= Tm1,m2,m3
+ rj
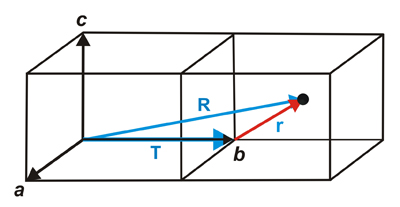Reducción
al interior de una celdilla unidad de la posición absoluta
de un
átomo, mediante translaciones de red
Al
estar el átomo incluído dentro de una celdilla,
sus
coordenadas
respecto de esa celdilla son de tamaño inferior a los ejes,
y se
suelen expresar en fracciones de los mismos:
r
= X a
+ Y b + Z c = X/a a
+ Y/b b + Z/c c
= x a + y b + z c
en
donde ya x,
y,
z,
como fracciones de eje, están comprendidos entre -1
y +1.
Entonces,
en las condiciones planteadas inicialmente, es decir, con un haz de
rayos X monocromático y despolarizado, de ondas planas,
formadas
por rayos paralelos de un frente de ondas común,
perpendicular
al
vector unitario de propagación s0
y
que baña completamente a la muestra, el modelo
cinemático de interacción indica que en
la muestra se
producen haces difractados en la dirección unitaria s
con
una intensidad:
I(H)
= Ie(H) IF(H)
IL(H)
en
donde
Ie es
la intensidad dispersada por un electrón, IL
es
el efecto de interferencia externa debido a la estructura
tridimensional
en red, e IF
es el cuadrado del llamado factor
de
estructura,
que viene a dar cuenta del efecto de interferencia interna debido a las
relaciones de fase geométrica entre todos los
átomos
incluídos
en la celdilla unidad. Este efecto de estructura interno es:
IF(H)
= | F2(H)
| = F(H)
F*(H)
pues,
debido a la representación compleja de las ondas, mencionada
al
principio, el cuadrado de un complejo se obtiene multiplicando al
complejo
por su conjugado.
Concretamente,
se llama factor
de estructura
F(H)
a la onda resultante de la dispersión provocada por
todos los átomos en una determinada dirección:
F(H)
= Σ(1
→ n) fj(H) exp
[2π(s
- s0)
rj
/ λ]
Ya
se dijo que los defases debidos a distancias geométricas R
son
proporcionales a (s
-
s0)
R
/ λ,
es
decir, que si cambiamos de origen, los defases serán
producidos
según la geometría del cambio, de forma que en
las
intensidades
las exponenciales de esos defases son complejas conjugadas y
sólo
afectan con una constante de proporcionalidad a las intensidades
totales.
Es decir, un cambio de origen no es relevante al fenómeno.
En
la expresión de la intensidad total,
I(H),
las condiciones de máximo debido a la repetición
en red,
traen como consecuencia que:
- El
fenómeno de difracción en muestras cristalinas
tiene
carácter
discreto, espectral.
- Las
direcciones y la repetición de la red que forma el espectro
no
dependen
del factor de estructura, es decir, sólo dependen de la red
directa.
El conocimiento de estas direcciones permite conocer la forma y el
tamaño
de la celdilla unidad directa, que así controla la
posición
de los máximos de difracción.
- La
intensidad de los máximos depende del valor del factor de
estructura
en esa dirección, es decir, en ese punto
recíproco, y
estos
máximos sólo dependen del contenido de la
distribución
atómica dentro de la celdilla unidad, que es lo que controla
las
intensidades de los máximos. Es decir, dan
información
sobre
la estructura atómica dentro de la celdilla unidad.
- El
espectro total de difracción es el efecto de
difracción
del
agregado atómico que forma la celdilla unidad muestreado en
los
puntos del espectro de difracción de la red cristalina que
lo
estructura.
- En
esencia, pues, la Cristalografía
estructural por difracción de rayos X,
consiste en medir las intensidades de la mayor cantidad posible de
haces
difractados del espectro tridimensional de difracción,
obtener
de
ellas los módulos de los factores de estructura, y de sus
valores,
mediante algún procedimiento de asignación de
fases a
cada
uno de estos factores, reconstruir la distribución
electrónica
en la celdilla elemental, cuyos máximos
corresponderán a
las posiciones atómicas.
Diagramas
de difracción de (a)
una
molécula, (b)
dos
moléculas, (c)
cuatro
moléculas, (d)
una línea
de moléculas repetidas
periódicamente, (e)
dos líneas
de moléculas y (f) una red
bidimensional periódica de moléculas.
Obsérvese,
cómo el espectro de esta última es el espectro de
la
molécula
muestreada en los puntos debidos al espectro de la red.
Para aclarar lo
expuesto
se pueden ver algunos objetos y sus correspondientes diagramas de
difracción
en análogos
ópticos.
Adicionalmente también
sugerimos al lector que observe el vídeo que
preparó la Royal
Institution para
demostrar
ópticamente el fundamento de la difracción con
una espiral de alambre y un láser.
Ecuaciones
de Laue, interpretación de Bragg y modelo
geométrico de
difracción
de Ewald
Hemos
visto que el diagrama de difracción de una red definida por
tres
translaciones a,
b
y c,
es
otra red definida por sus
translaciones
recíprocas:
a*,
b*
y
c*.
Los vectores de translación que definen estas dos redes
(directa
y recíproca) cumplen las condiciones de reciprocidad:
a
a* = b b*
= c c*
=
1 y
a
b*
= a c* =
b c* = 0
y
son de forma que:
a*
= (b x
c)
/ V
(x
significa
producto vectorial)
siendo
V
el
volumen de la celdilla definida por los tres vectores de la red
directa,
y por lo tanto:
a*
= N100
/ d100
siendo
N100
un
vector unitario perpendicular a la secuencia de planos de
índices
h=1,
k=0,
l=0,
y
d100
el
espaciado interplanar correspondiente. Y análogamente con b*
y c*.
De
esta manera, cualquier vector de la red recíproca
vendrá
dado por:
H*hkl
= h a*
+ k b*
+ l c*
= Nhkl
/ dhkl
de
modo que:
|H*hkl|
dhkl
= 1
Por
otro lado, hemos visto que los máximos del diagrama de
difracción
de una muestra cristalina corresponden a máximos de la
función
IL(H),
es decir, que cada uno de los productos que definen esta
función
han de ser, individualmente, distintos de cero para obtener una
condición
suficiente de máximo de intensidad difractada. Es
decir, que
han
de cumplirse las llamadas tres ecuaciones de Max von Laue (1879-1960)
[recordemos que H
= (s
- s0) /
λ]:
H a
= h,
H b
=
k, H c = l
siendo
h,
k, l
números
enteros
Ecuaciones
de Laue
Existe un
modo algo menos
formal
para deducir y/o interpretar las Ecuaciones de Laue, y para ello
invitamos al lector interesado a visitar este enlace...
Estas tres
condiciones
de Laue se cumplen siempre que el vector H
sea
un vector de la red recíproca H*,
de forma que sea:
H
= h a* + k
b*
+ l c*
pues, debido a las
propiedades
de la red recíproca, se cumplirá que:
Hhkl
a =
h,
Hhkl
b
= k,
Hhkl
c
=
l
Es
decir, que las tres condiciones de
Laue
(
Premio Nobel de Física en 1914)
son equivalentes a establecer que el vector
H
sea un vector de la red recíproca
(
H
=H*hkl).
En
estas condiciones de máximo, y con las relaciones expuestas
anteriormente,
tendríamos:
| H
| = 2 sen θhkl
/ λ = | (s
- s0)
|
/ λ =
| H*hkl
|
= 1
/ dhkl
Pero teniendo en cuenta que
geométricamente se pueden considerar espaciados del
tipo dhkl/2,
dhkl/3,
y
en general, dhkl/n (es
decir, dnh,nk,nl, siendo n
un número entero) la ecuación de Bragg (Premio Nobel de
Física en 1915)
quedaría en la
forma:
λ =
2 (dhkl /n)
sen θnh,nk,nl
es decir:
n λ =
2 dhkl
sen θnh,nk,nl
en donde n
es un
número entero
Ley
de Bragg
Existe un
modo algo menos
formal
para deducir y/o interpretar la ley de Bragg, y para ello
invitamos al lector interesado a visitar este enlace...
Además, si se
cumplen las condiciones de Laue, y según se explica en la
figura siguiente,
todos los átomos, situados sobre la secuencia de planos
paralelos
a uno dado de índices hkl
con distancia al origen DP
que sea un múltiplo entero de dhkl,
difractarán en fase, pues el factor de defase
geométrico
será:
(s
- s0)
r
= n λ
y
se producirá un máximo de intensidad en la
dirección
de difracción:
s =
s0
+ λ
H*hkl
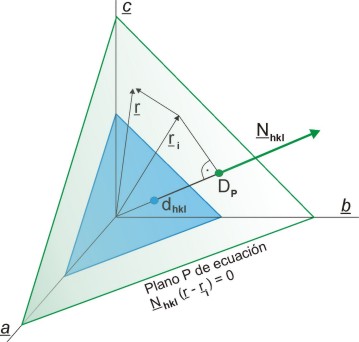
Geometría
del modelo que interpreta la difracción en fase de todas las
secuencias
de planos correspondientes a un triplete de índices hkl y
de
espaciado
constante dhkl,
cuando se alcanzan las condiciones de Laue, o su equivalente de Bragg. Nhkl es
el vector unitario normal a toda la secuencia de planos que, como hemos
visto, en condiciones de máximo de difracción,
viene dado
por:
Nhkl
= H*hkl
dhkl
y la ecuación del
plano queda, pues:
H*hkl
r
= H*hkl
ri=
|H*hkl|
|ri|
cos (H*hkl
, ri)
= (1/dhkl) DP = n
La ecuación
de
Bragg tiene una interpretación sencilla, y es que cuando en
la
interacción
cristal-radiación se produce una situación de
máximo
de difracción, el fenómeno es como
si la radiación incidente se estuviera reflejando en
la secuencia de planos cristalinos de índices
hkl
y
espaciado dhkl.
Es
por eso por lo que, hablando de máximos de
difracción, se
use
a veces la palabra reflexión
de Bragg. Por otro lado, esta
ecuación
encierra las típicas relaciones de reciprocidad de la
difracción,
entre espaciado
- dirección
ó entre posición
- momento.
A menor espaciado, mayor ángulo y viceversa; redes directas
con
celdillas elementales grandes producen haces muy próximos, y
al
revés.
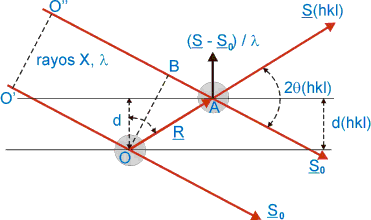
La
figura representa la descripción geométrica de la
dirección
del máximo de difracción debido a la
interferencia
constructiva
entre los átomos de los planos de espaciado d(hkl).
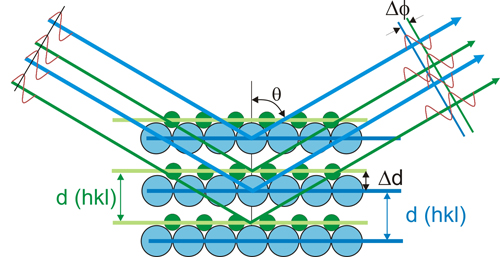
La figura da una
descripción del modelo de Bragg cuando
se
trata
de secuencias de planos del mismo espaciado, pero formados a su vez por
átomos de distinto tipo, separados por Δd.
Esta
separación geométrica origina diferencias de fase
dentro
de un mismo haz difractado que provocan interferencias y que dan lugar
a variaciones de intensidad (según la dirección),
lo que permite obtener información de la estructura de los
átomos que forman el cristal.
El usuario que lo desee, y que
disponga de
las herramientas de Java Runtime
instaladas, puede "jugar"
con el modelo de
Bragg, usando
este "Applet".
Por otra parte, hemos
visto
que, en general:
H
= (s - s0)
/ λ
= -s0/λ
+ s/λ
es
decir, que los
vectores
H
pueden considerarse como pertenecientes a una esfera de radio 1/λ
centrada
en el punto definido por el vector -s0/λ
respecto
del origen donde se sitúa el cristal. Esta es la llamada esfera
de Ewald (1921),
que
proporciona
una interpretación geométrica, también
sencilla,
para
las posiciones de máximo de difracción, pues
cuando los
vectores
H
pertenecen
a la red recíproca y ésta corta a la
esfera de
Ewald, se producen máximos de difracción, y el
cristal
queda
situado en posición de Bragg.
Resulta
sorprendente la rapidez con la que Paul
Peter Ewald (1888-1985) desarrolló
toda
esta interpretación, tal como publicó
apenas unos
meses después de los experimentos de Max
von Laue y que se pueden consultar a través de este enlace en el
artículo original publicado en 1913. El
lector interesado puede
igualmente consultar el artículo publicado por este autor en
Acta
Crystallographica (1969) A25, 103-108.
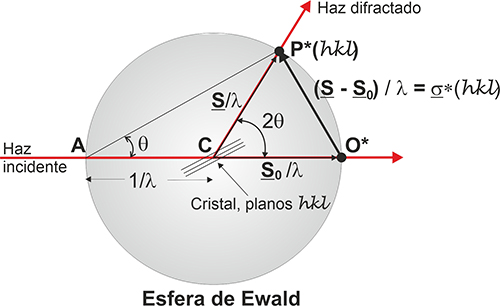
La
figura describe el modelo geométrico de Ewald. Cuando un
punto recíproco P(hkl) toca a
la esfera, se produce un
haz
difractado
en la dirección que une el centro de la esfera con el punto
de
corte.
Realmente, el origen de la red recíproca O*
coincide
con la posición del cristal y los haces difractados salen de
ese
origen común, pero paralelos a los definidos en la figura y
tal
como se representa en la figura de abajo.
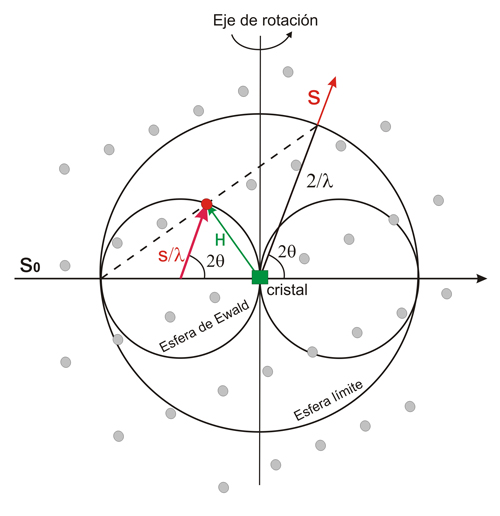
En
esta figura aparece todo el volumen recíproco que puede dar
lugar
a máximos de difracción al girar la muestra.
Cambiando
las
orientaciones, se pueden recoger todos los haces correspondientes al
espacio
recíproco contenido en una esfera de radio 2/λ,
que
se denomina esfera
límite. Los puntos recíprocos se
muestran como pequeñas esferas grises.
Para
obtener todos
los
máximos de difracción que pueda proporcionar una
muestra
cristalina, bajo radiación de longitud de onda λ,
basta
con orientar convenientemente el cristal (y por tanto la red
recíproca
que lo acompaña) y hacerlo girar de modo que sus puntos
corten a
la esfera de Ewald. A lo largo de estos puntos de corte se
producirán
los máximos de difracción. Para longitudes de
onda
largas,
la parte explorada de la red recíproca será menor
que
para
longitudes de onda más cortas; sin embargo, los haces
difractados
quedarán más separados entre sí para
longitudes de
onda más largas.
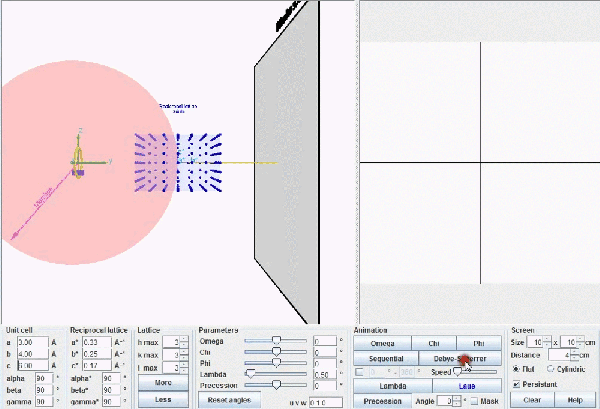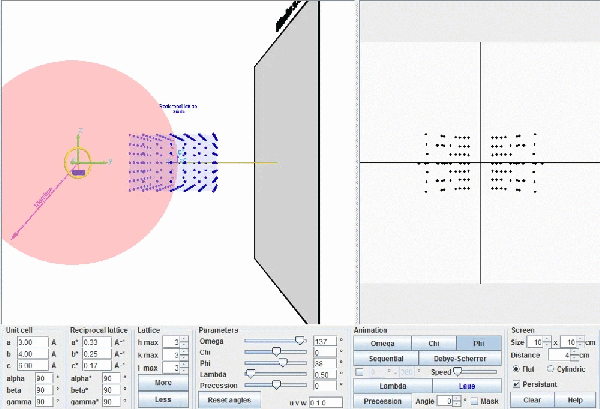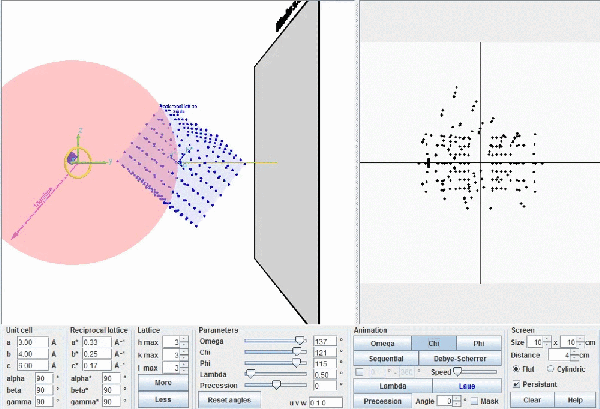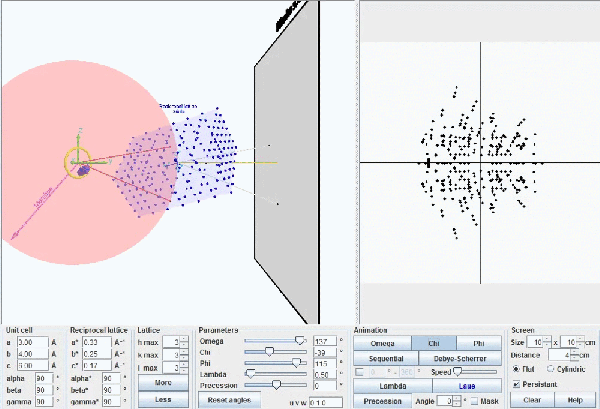
Modelo
de Ewald dando cuenta de la difracción. Los
rayos X incidentes, de longitud de onda λ,
(línea
blanca)
llevan asociados una esfera imaginaria (verde)
de
diámetro 2/λ.
La
red recíproca (puntos
rojos) se mueve solidariamente con el
cristal,
y cada vez que un punto recíproco choca con la superficie de
la
esfera se provoca un haz difractado que emerge desde el
centro de
la esfera y que pasa por el punto (líneas amarillas).
Modelo
de Ewald, idéntico al mostrado en la figura superior, pero
en
dos dimensiones, y mostrando el detector en donde se recogen los haces
difractados
Tomado de Philip Willmott (Paul Scherrer Institute, Suiza)
Puede resultar también
ilustrativa esta aplicación
Java que el lector puede descargar desde este enlace totalmente libre de virus.
Dicha
aplicación, que también se basa en el concepto de
la red
recíproca, permite "jugar" con el modelo de Ewald
para interpretar la difracción. El "applet" es original
de Nicolas Schoeni y Gervais Chapuis de la
Ecole Polytechnique Fédéral de Lausanne (Suiza).
Según la
ley
de
Bragg, el máximo ángulo al que se puede
obtener
la
difracción
corresponde al valor máximo de la función seno
(la
unidad),
es decir, que la máxima
resolución
teórica
que se puede alcanzar entre
átomos es
de λ/2.
En
la práctica, debido a la disminución de los
factores
atómicos
de dispersión cuando aumenta el ángulo de Bragg,
sólo
aparecen intensidades apreciables hasta un valor
máximo θmax
< 90º
y la
resolución
práctica
que se alcanza
será dmin
= λ/2
sen θmax.
Si se considera que dhkl
es
una constante de la muestra, al disminuir la longitud de onda
incidente, la
ecuación
de Bragg nos indica que los ángulos de difracción
(θ) serán
menores y por lo tanto el espectro se contrae, pero por contra se
pueden obtener más órdenes
de difracción y disponer así de mayor
resolución estructural.
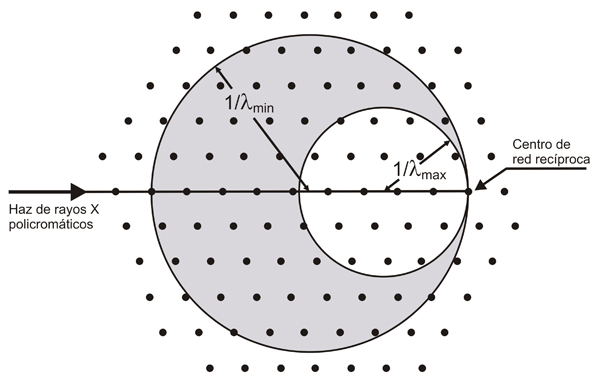
Según
el modelo de Ewald, la zona medible del espacio recíproco
aumenta al disminuir la longitud de onda, es decir, al aumentar el
radio de la esfera de Ewald
Resulta
también muy pedagógico visitar las
páginas que sobre espacio
recíproco se ofrecen desde la Universidad
de Cambridge a través de este enlace,
así como el
vídeo realizado por www.PhysicsReimagined.com,
que muestra las relaciones geométricas entre las redes
directa y
recíproca, y que aquí mostramos como gif animado:
Una
vez establecidos
los
fundamentos del modelo teórico que da cuenta del
fenómeno
de la difracción en monocristales, animamos al lector a
visitar
las páginas que se dedican a los distintos
métodos
experimentales
de medida de las intensidades de difracción.
Siguiente
capítulo:
Difracción experimental
Tabla
de contenido
Esta
es la
ecuación
de Bragg [William
L. Bragg (1890-1971)] que
se puede expresar en la forma habitual:
