 Las
ecuaciones de Max
von Laue (1879-1960)
describen el comportamiento de las ondas que son difractadas al
incidir sobre una red cristalina. Pueden deducirse de un
modo algo menos formal que lo hizo el propio autor, pero de un modo
relativamente intuitivo...
Las
ecuaciones de Max
von Laue (1879-1960)
describen el comportamiento de las ondas que son difractadas al
incidir sobre una red cristalina. Pueden deducirse de un
modo algo menos formal que lo hizo el propio autor, pero de un modo
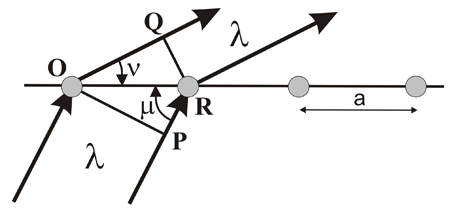
relativamente intuitivo...Basta para ello considerar una hilera de átomos, regularmente distanciados, tal como muestra la figura de la izquierda y considerar, como hipótesis, que un frente de ondas (OP) que incide sobre la línea de átomos se dispersa cooperativamente (se difracta) al otro lado de la línea citada y genera otro frente de ondas (QR) cuya dirección de propagación habrá cambiado.
Por lo tanto, si en el frente de ondas QR se observa dispersión cooperativa (difracción), es porque los dos haces que lo componen están en fase, o lo que es lo mismo, que la diferencia de caminos recorridos por los haces OQ y PR es un número entero (m) de longitudes de onda (λ), es decir:
OQ
- PR = m λ
y como:
cos ν = OQ / a
cos μ = PR / a
Si nos fijamos con atención en esta última ecuación, no resultará dificil darnos cuenta de que:
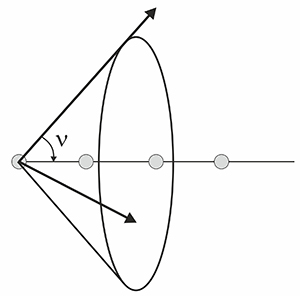
Dispersión por una hilera de átomos distanciados regularmente
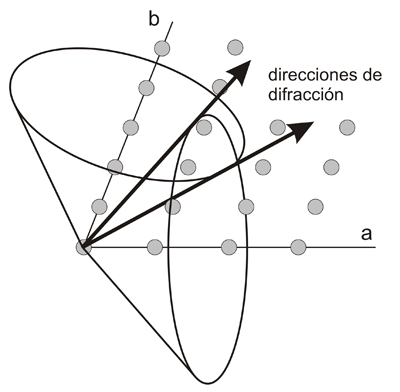
Dispersión cooperativa (difracción) por dos hileras de átomos distanciados regularmente
El hecho de que se cumplan simultáneamente estas dos ecuaciones equivale a considerar como válidos exclusivamente los puntos comunes de ambos conos, es decir, sus intersecciones, que son dos líneas rectas. Dicho de otro modo, la dispersión cooperativa (difracción) de dos líneas no paralelas de átomos (y en general de un plano de átomos) se reduce sólo a líneas discretas de difracción.
Generalizando a cualquier distribución periódica de átomos en 3 dimensiones, habremos de considerar que se deberán cumplir tres ecuaciones como las mostradas más arriba, es decir:
en donde m, n, p son tres números enteros, y constituyen las denominadas Ecuaciones de Laue.
cos μ = PR / a
resulta:
a
(cos ν - cos μ) =
m λ
Si nos fijamos con atención en esta última ecuación, no resultará dificil darnos cuenta de que:
- No hay órdenes fraccionarios de dispersión cooperativa, ya que el número m es un entero, y
- Si se mantiene constante el ángulo de incidencia μ, esta ecuación será igualmente válida para cualquier haz dispersado que mantenga el mismo ángulo de salida (ν), y por lo tanto el lugar geométrico común a todos esos haces dispersados formará una superficie cónica, coaxial con la linea de átomos (véase la figura siguiente)...

Dispersión por una hilera de átomos distanciados regularmente

Dispersión cooperativa (difracción) por dos hileras de átomos distanciados regularmente
En
el caso
bidimensional, es decir,
si consideramos dos hileras de átomos, tales como las
marcadas
con las letras a
y b (figura
de arriba), es de esperar que cada
una de ellas disperse los rayos X en la forma descrita más
arriba, es decir, en forma de conos coaxiales con dichas hileras. Pero
para que finalmente ambas dispersiones sean cooperativas (que exista
difracción) se habrán de cumplir
simultáneamente
dos ecuaciones equivalentes a la mostrada más arriba, es
decir:
a (cos ν1 - cos μ1) =
m λ
b (cos ν2 - cos
μ2) = n λ
El hecho de que se cumplan simultáneamente estas dos ecuaciones equivale a considerar como válidos exclusivamente los puntos comunes de ambos conos, es decir, sus intersecciones, que son dos líneas rectas. Dicho de otro modo, la dispersión cooperativa (difracción) de dos líneas no paralelas de átomos (y en general de un plano de átomos) se reduce sólo a líneas discretas de difracción.
Generalizando a cualquier distribución periódica de átomos en 3 dimensiones, habremos de considerar que se deberán cumplir tres ecuaciones como las mostradas más arriba, es decir:
a (cos
ν1 - cos μ1) =
m λ
b (cos ν2 - cos μ2) = n λ
b (cos ν2 - cos μ2) = n λ
c (cos
ν3
- cos μ3) = p
λ
en donde m, n, p son tres números enteros, y constituyen las denominadas Ecuaciones de Laue.
