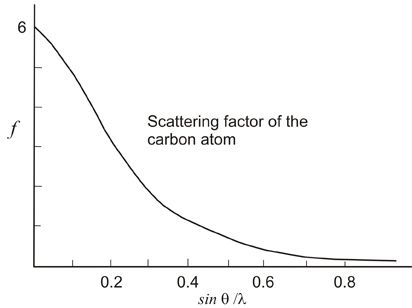
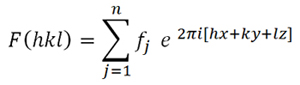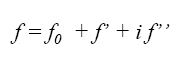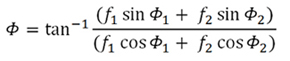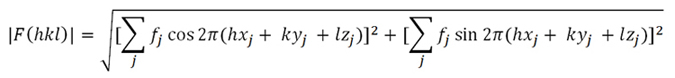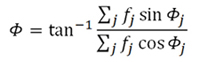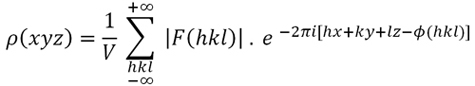As mentioned above,
a structure factor, F(hkl),
is the resultant of all waves scattered in the direction of the hkl
reflection
by the n atoms contained in the unit cell.
Its mathematical expression must therefore take into account the
scattering from every atom contained in it.
But let's see how we can get the mathematical expression that
defines it ...
Analytical expression of the phase
Suppose
a crystal formed by the repetition of the atomic model constituted by
the pair of atoms (red and blue) shown in the left figure. Of course,
any crystalline model can be decomposed into as many simple lattices as
atoms (look at the two lattices drawn below, red
and blue).
Any crystalline model can be decomposed into simple lattices...
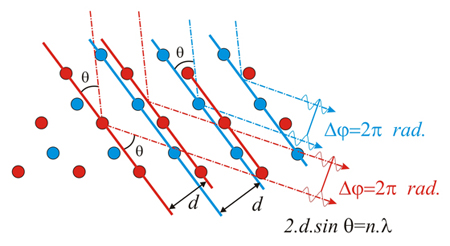 If the Bragg's
Law
is true, the phase difference between the two reflected red beams will
be 0° (= 360° = 2π radians). And the same will
happen for the two reflected blue beams.
If the Bragg's
Law
is true, the phase difference between the two reflected red beams will
be 0° (= 360° = 2π radians). And the same will
happen for the two reflected blue beams.
However, since
there is
a separation
between the two
lattices, there will be a phase shift
between red and blue waves. and therefore the total diffracted
intensity will be less than the arithmetic sum of both, red + blue
intensities.
The resulting amplitude (ie the diffraction intensity) is controlled by
the
separation between the two lattices (ie by the shape of the motif being
repeated), while the resulting diffraction geometry is the same as the
one produced by of each single lattice. The diffraction geometry
depends only on the lattice geometry.
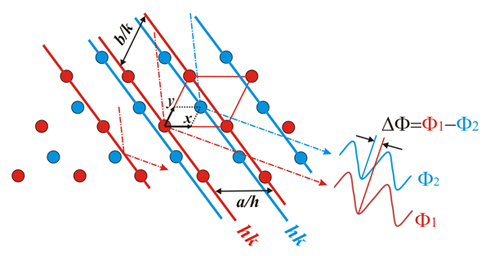 The red
X-ray beams, which are being
reflected on the red planes of indices hk, fulfill the Bragg's Law, and in the
same manner will behave the blue beams on the blue planes hk.
Said in other words,
if Bragg's Law is fulfilled, the phase shift between waves
reflected on planes of the same color, shifted (a/h)
in the direction of the a-axis,
must be 2π = 360º. For the same reason, the phase
difference due to the plane separation (b/k)
in the direction f the b-axis
must also be 2π = 360º.
The red
X-ray beams, which are being
reflected on the red planes of indices hk, fulfill the Bragg's Law, and in the
same manner will behave the blue beams on the blue planes hk.
Said in other words,
if Bragg's Law is fulfilled, the phase shift between waves
reflected on planes of the same color, shifted (a/h)
in the direction of the a-axis,
must be 2π = 360º. For the same reason, the phase
difference due to the plane separation (b/k)
in the direction f the b-axis
must also be 2π = 360º.
But the beams reflected on the blue planes show a phase shift respect
to the red ones by a quantity (ΔΦ radians) that
depends on
the separation between the two lattices...
In fact, this offset
can be
easily calculated using the following "rule of three" proportions,
applied to the three
independent space directions:
a/h .....
2π
b/k .....
2π
c/l .....
2π
x
..... ΔΦa
y
..... ΔΦb
z ..... ΔΦ
ΔΦa = 2π h x/a
ΔΦb = 2π
k
y/b
ΔΦc = 2π
l
z/c
Combining the three
phase shifts, and generalizing to the three dimensions:
ΔΦ = 2π (h x/a + k y/b + l z/c)
Finally, taking fractional
coordinates (that is, assuming x=x/a,
y=y/b,
z=z/c) and replacing
ΔΦ by Φ:
Φ = 2π (h x + k y + l z)
radians
(Formula 1)
Analytical expression of the
structure factor
 Once the
mathematical expression of the phase is established in terms of the
shape of the crystalographic model (Formula 1),
let's see how to arrive at the analytical expression of the structure
factor...
Once the
mathematical expression of the phase is established in terms of the
shape of the crystalographic model (Formula 1),
let's see how to arrive at the analytical expression of the structure
factor...
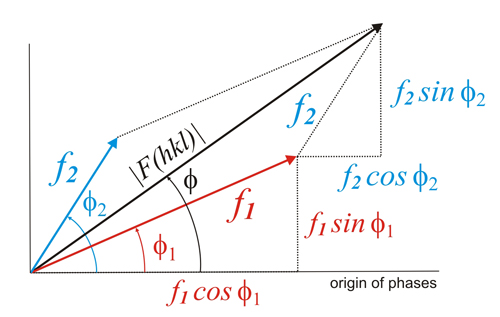
Suppose
that ƒ1
represents the dispersion of the red atoms, and ƒ2
for the blue atoms (figure on the left). The total resultant dispersion
of both atom types will be F(hkl)...
Writing it using vector notation...
F(hkl) = ƒ1 + ƒ2
According
to the scheme shown on the left, the module of
this vector sum will
be:
and its phase, referred to
an arbitary phase origin:
Generalizing now for all atoms, and taking into account the general
expression for the phase (Formula 1,
above), the module of the structure factor will be:
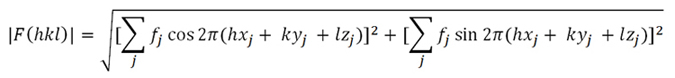 (Formula 2)
(Formula 2)
We have used the vector graphic representation to deal with
diffraction waves, and this is equivalent to considering that waves can
be represented as complex numbers. In this type of representation, the
real and imaginary parts correspond to the projections of the wave
amplitude on the cartesian axes, and the phase is the angle
that
forms the vector with the horizontal axis, which acts as an origin to
which phases are referred.
Therefore,
and taking into account Formula 2,
the complex expression for the structure factor will be:

which,
according to Euler's
formula, can also be written as:
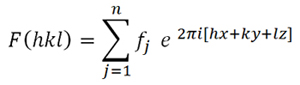
Formula 3.
The structure factor as a complex number
Evaluation of structure factors
If we know the internal structure of any crystal, ie the types of atoms
(ƒj) that constitute it, and the
positions (x,y,z) of all atoms (n) contained in the unit cell, we can
immediatly calculate the structure factors, F(hkl),
that define the crystal.
To do this, it is enough to apply Formula 3,
which actually involves calculating the inverse Fourier
transform of the electron
density function:
Fórmula 4.
The
electron density function defined at the point (x, y, z) in the unit
cell
The structure factors calculated with Formula 3
above, ie from the known atomic structure, are represented by vectors (modules and phases)
and their numerical values, corresponding to the so-called absolute
scale, since they are calculated with the dispersion factors (ƒj) that depend on the atomic numbers of
the atoms existing in the unit cell.
However, the conventional situation is the opposite one. That is, we
normally pretend to solve Formula 4,
to determine the structure of the crystal by solving the function of
electronic density at each point of the unit cell. And for this purpose
we have to measure experimentally the structure factors using the X-ray
diffraction. However, we must remember that experimentally we can only
measure their modules, and therefore we have to face the so-called phase
problem.
The modules of the experimental structure factors are related to the intensities
of the diffracted beams,
but these are in a relative scale, since they depend on multiple
experimental aspects, such as the crystal dimensions and the brightness
of the primary X-ray beam.
But let's
go back...


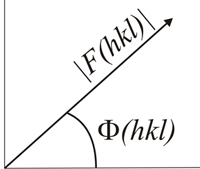 Analytically
speaking, each structure factor can be considered as a vector, with its
amplitude and phase (referred to an arbitrary origin of
phases),
and represents the total wave resulting from the co-operative
dispersion (diffraction), caused by all the atoms of the cell, in a
given direction of space.
Analytically
speaking, each structure factor can be considered as a vector, with its
amplitude and phase (referred to an arbitrary origin of
phases),
and represents the total wave resulting from the co-operative
dispersion (diffraction), caused by all the atoms of the cell, in a
given direction of space.