Simetría de los cristales.
Teorema
de restricción cristalográfica
En otro apartado se ha indicado
que los ejes de
simetría en los cristales sólo responden a
órdenes de rotación 2, 3, 4 y 6. Pues
bien,
aunque los objetos aislados pueden mostrar ejes de simetría
de orden 5,
7, 8 (o superior) estos
órdenes de
rotación no son compatibles con la repetición
cristalina. La razón para esta incompatibilidad hay que
encontrarla en el hecho de que la forma externa de
los cristales es consecuencia de la disposición
geométrica ordenada de los átomos. En efecto, si
uno intenta combinar objetos con ejes de rotación de orden
5, 7, 8 (o superior) nos
daremos cuenta de que es imposible rellenar
totalmente el espacio, tal como se ilustra a continuación:
Empaquetamiento de objetos con ejes
de rotación de orden 5
y 8. No llenan el
espacio, por lo que estos elementos de simetría son
incompatibles con los retículos
cristalinos.
Al margen de las consideraciones
de
empaquetamiento, es sencillo demostrar
geométricamente la
imposibilidad de existencia de ejes de rotación de orden 5 en
los cristales. Supongamos una red que cumpliera la simetría
de
orden 5,
tal como se muestra en la figura siguiente, con los
supuestos puntos reticulares como círculos grises. Si ello
fuera
así, por definición de retículo, la
suma de
cualquier pareja de vectores que definen los puntos reticulares
debería generar un nuevo punto reticular. Si sumamos los
vectores t1
y t4 nos daremos cuenta
de que no obtenemos t5,
sino un nuevo vector (t1
+ t4, en rojo) con traslación no
reticular, lo cual inhabilita la hipótesis de partida.
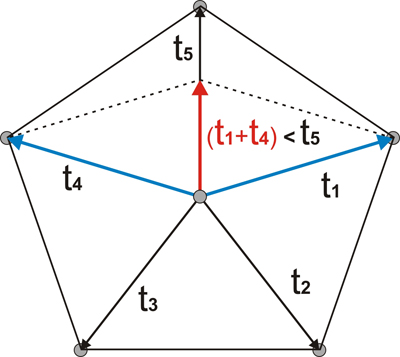
Demostración
geométrica de la imposibilidad de un retículo con
simetría de orden 5
Desde un punto de vista algo más formal es
también facil deducir esta restricción en los
órdenes de rotación (n) de los ejes de
simetría de los cristales. Consideremos una línea
reticular, con puntos separados por el vector de traslación t
(círculos grises en
la figura de más abajo).
Si a dicha línea (la de círculos grises) le
aplicamos una supuesta
operación de simetría rotacional de orden n, con
giro +α
(=360º/n)
perpendicular al plano del dibujo, obtendremos la línea de
círculos azules. Y
aplicando la operación de rotación inversa, -α
obtendremos la línea de círculos rojos.
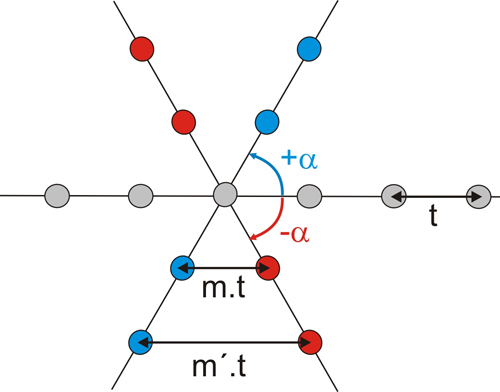
Aplicación de un eje de
rotación de orden n a una línea reticular
(círculos grises)
Para que la operación de giro +α
sea realmente una
operación de simetría de la red, los
círculos
azules deberán corresponden a puntos del
retículo, e igualmente debería ocurrir con los
círculos rojos. Pero además, las distancias entre
los
círculos
azules y rojos deberán ser múltiplos de t (la
traslación reticular), es decir, deberán ser del
tipo: m.t, m’.t,
etc., siendo m, m’, números enteros.
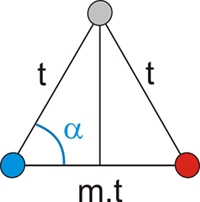
En el triángulo isósceles que se obtiene tras
los
giros de la mencionada línea reticular (figura
inmediatamente superior), deberá cumplirse que:
cos α =
(1/2) m.t / t
o
lo que es lo mismo:
cos α =
m / 2
y puesto que los valores de la función coseno deben estar
comprendidos entre -1
y +1, sólo están
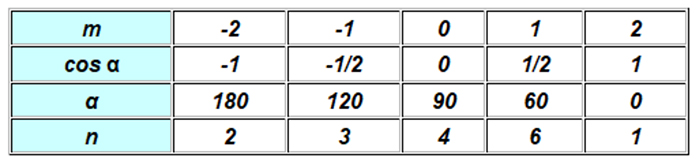
permitidas cinco posibilidades, que corresponden a los
ejes de
rotación de orden, 2,
3, 4, 6 y 1
(rotación de 0º o 360º):
lo que constituye el
denominado teorema de restricción cristalográfica.
Pero volvamos
al punto de partida...
