The symmetry of crystals. The
crystallographic
restriction theorem
Although objects themselves may
appear to have
5-fold, 7-fold, 8-fold, or
higher-fold rotation axes, these are not
possible in crystals. Crystals can only
show 2-fold,
3-fold, 4-fold or 6-fold rotation axes.
The reason is that the external shape
of a
crystal is based on a geometric arrangement of atoms. In fact, if we
try to combine objects with 5-fold
and 8-fold
apparent
symmetry, we cannot combine them in such a way that they
completely fill space, as illustrated below:
Packing
of objects displaying 5-
and 8-fold
symmetry. Note that they do not
fill completely the space and therefore these symmetry elements are not
compatible with
crystal lattices..
If we assume that 5-fold
symmetry is possible, we would be able to draw the grid points shown
below as small gray circles, defined by the shortest translation
vectors t1
= t2
= t3
= t4
= t5.
The sum of any two lattice vectors must also be a lattice
vector, but no lattice vector can be shorter than the shortest lattice
vectors we have just set up. In fact, if we take the sum of the t1
and t4
vectors we will get a new vector (t1
+ t4, shown in red) whose
magnitude is less than our “shortest” lattice
vectors, what
destroys the hypothesis.
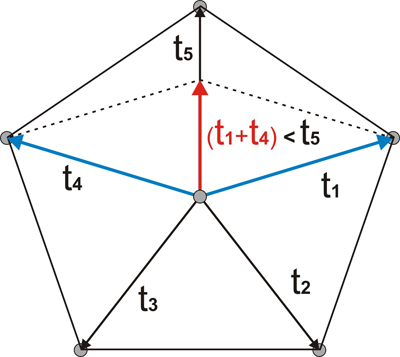
Geometric
proof of the impossibility of a lattice with 5-fold symmetry
Consider a grid line with lattice points (gray circles) separated by a
translation vector t
(see below). If we rotate the line around a symmetry axis of order n (perpendicular to
the drawing), +α
(=360º/n), we will get the line with blue circles.
And similarly, applying the reverse rotation, -α we will get the line of red circles.
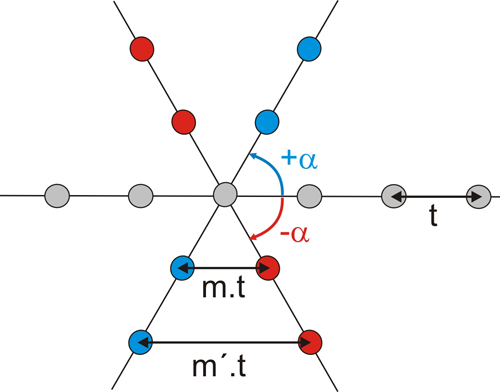
Applying a rotation axis of order n to a grid line (gray circles)
If the α
rotation is a lattice symmetry operation, the blue circles will
correspond to lattice points, and similarly will occur with the red
circles. And if this is so, any distance between blue and red circles
must be equal to an integral multiple of the lattice translation (t): m.t, m'.t, etc., where m is an integer.
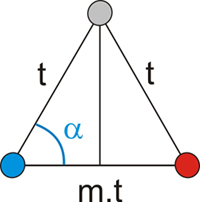
In
the isosceles triangle (obtained after rotating the grid line) the
following expression can be written:
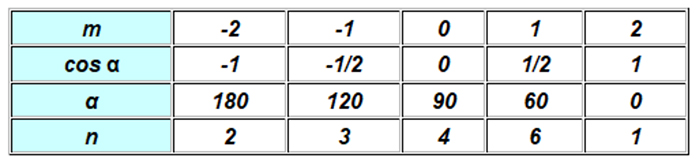
cos α =
(1/2) m.t / t
that
is:
And since the value of the cosine
function must be between -1
and +1, only five possibilities will be
allowed, corresponding to the rotation axes of order 2, 3, 4, 6 and 1 (rotation of
0º or 360º):
But let's go
back...
