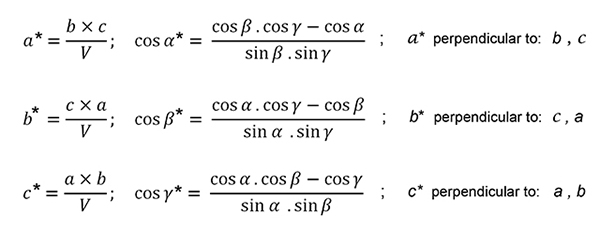4. Direct and
reciprocal lattices

Let's
start with a summary of several concepts seen in previous chapters...
Any repetitive and
periodic distribution of a set
of objects (or motifs)
can be characterized, or described, by translations
that repeat the set of objects periodically. The implied
translations
generate what we call a direct
lattice (or real
lattice).


Left:
Fragment
of a distribution of
a set of objects that produce a direct lattice in 2 dimensions. As an
example, one of the infinite sets of motifs (small tiles) that
produce the repetitive and periodic distribution is shown inside the
yellow squares. The dimensions of the yellow square represent the
translations of the direct lattice
Right:
Fragment of a mosaic in La
Alhambra
showing a 2-dimensional periodic pattern. These periodic translations
can be discovered in the mosaic and produce a 2-dimensional direct
lattice. The red square represents the translations of the smallest
direct lattice produced by the periodic distributions of the small
pieces of this mosaic.The yellow square represents another possible
lattice, a bigger one, non primitive.
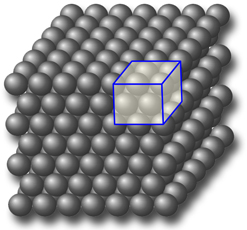
Periodic
stacking of balls, producing a 3-dimensional network (direct lattice).
The motif being repeated in the three directions of space is the
contents of the small box with blue edges, the so called "unit
cell".
The translations that describe the periodicity in crystals can be
expressed as a linear combination of three basic translations, not
coplanar, ie independent, known as reticular
or lattice axes
(or unit cell axes). These axes define a parallelogram (in 2
dimensions), or a parallelepiped (in 3 dimensions) known as a unit
cell (or
elementary cell). This elementary area (in 2-dimensional
cases), or elementary volume (in 3-dimensional
cases), which holds the
minimum set of the periodic distribution, generates (by
translations) the full distribution which, in our
atomic 3-dimensional
case, we call crystal.
In addition to the fact that the unit
cell
is the smallest repetitive unit as far as translations is concerned,
the reader should note that the system of axes defining the unit cell
actually defines the reference system to describe the positional
coordinates of each atom within the cell.
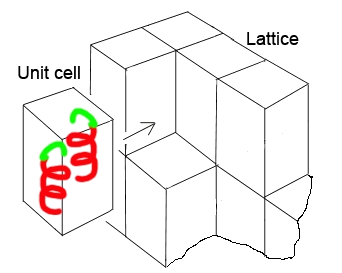
Left: Elementary
cell (or unit cell) defined by the 3 non-coplanar reticular
translations (cell axes or lattice axes)
Right: Crystal formation by stacking of many
unit cells in 3 space directions
In
general, inside the unit cell there is a minimum set of atoms (ions or
molecules) which are repeated inside the cell due to the symmetry
elements of the crystal structure. This minimum set of atoms
(ions or molecules) which generate the whole contents of the unit
cell (after applying the symmetry
elements to
them) is known as the asymmetric
unit.

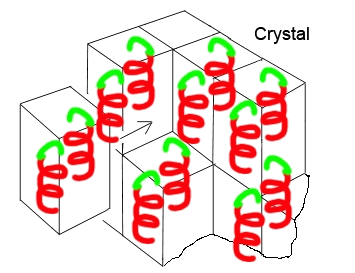
 The structural
motif shown in
the left figure is repeated by a symmetry element (symmetry operation),
in this case a screw axis
The repetition of the motif (asymmetric
unit) generates the full content of the unit cell, and the
repetition of unit cells generates the entire crystal
The structural
motif shown in
the left figure is repeated by a symmetry element (symmetry operation),
in this case a screw axis
The repetition of the motif (asymmetric
unit) generates the full content of the unit cell, and the
repetition of unit cells generates the entire crystal
The lattice, which is a pure
mathematical
concept, can be selected in various ways in the same real periodic
distribution. However, only one of these lattices "fits"
best with the symmetry of the periodic distribution of the
motifs...
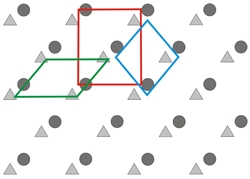
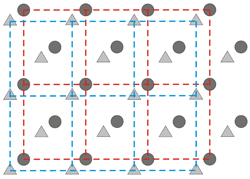
Two-dimensional periodic distribution of
one motif containing two objects (a triangle and a circle)
Left: Unit
cells corresponding to possible direct lattices (=real lattices) that
can be drawn over
the periodic distribution shown above. Only one of the unit cells (the
red one) is more appropriate because it fits much better with the
symmetry
of the distribution
Right: The red
cell on the left figure (a centered lattice) fits better with
the
symmetry of the distribution, and can be decomposed in two identical
lattices, one for each object of the motif.
As is shown in the figures above,
although especially in the right one, any
lattice that describes the repetition of the motif
(triangle + circle) can be decomposed into two identical equivalent
lattices (one for each object of the motif). Thus, the concept of
lattice is independent of the complexity of the motif, so that
we can use only one lattice, since it represents all the
remaining
equivalent ones.
Once we have chosen a
representative
lattice, appropriate to the symmetry of the structure, any reticular
point (or lattice
node) can be described by a vector that is
a linear combination (with integer numbers) of the
direct reticular axes: R
= m
a
+ n
b
+ p
c,
where m,
n and
p
are integers. Non-reticular points
can be reached using the nearest R
vector, and adding to it the corresponding fractions of the reticular
axes to reach it:
r
= R
+ r'
= (m a
+ n b
+ p c)
+ (x a
+ y b
+ z c)
Position vector for
any non-reticular point of a direct lattice
where x,
y,
z
represent the corresponding dimensionless fractions of axes X/a,
Y/b,
Z/c,
and X,
Y,
Z
the corresponding lengths.
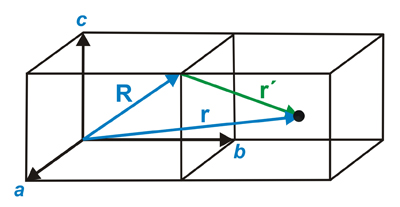 Position vector for a non-reticular point
(black circle)
Position vector for a non-reticular point
(black circle)
The reader should
also have a
look into the chapters about lattices
and unit
cells offered by the
University of Cambridge.
Alternatively, the
reader can download
and run on his own computer this Java application that
illustrates the lattice concept
(it is totally virus free and was developed by Gervais Chapuis and
Nicolas Schöni, École Polytechnique
Fédérale
de Lausanne, Switzerland).
Let's
now see some new concepts on direct
lattices (= real
lattices) ...
From a geometric point of view, on a
lattice we can consider some reticular
lines and reticular
planes which are those passing through the reticular
points (or reticular nodes).
Just as we did with
the lattices
(choosing one of them from all
the equivalent ones), we do the same with the reticular lines and
planes. A reticular line or a reticular plane can be used as a
representative of the entire family of parallel lines or parallel
planes.
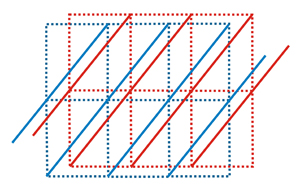
Following
with the argument given above, each motif in a repetitive distribution
generates its own lattice, although all these lattices are identical (red and blue). Of
the two families of equivalent
lattices shown (red and blue)
we can choose only one of them, on the understanding that it
also represents the remaining equivalent ones. Note that the distance
between the planes drawn on each lattice (interplanar
spacing) is the same
for the blue
or red
families. However, the family of red planes is
separated from the family of blue
planes by a distance that depends on the separation between
the
objects which produced the lattice. This distance between the planes of
different families can be called the geometric
out-of-phase distance.
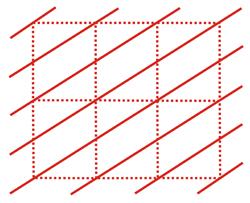
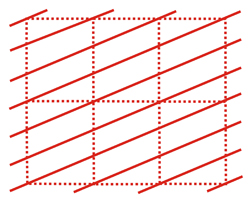
Left:
Family
of reticular planes cutting the
vertical axis of the cell in 2
parts and the horizontal axis in 1
part. These planes are parallel to the third reticular axis (not shown
in the figure).
Right: Family of
reticular planes cutting the
vertical axis of the cell in 3
parts and the horizontal axis in 1
part. These planes are parallel to the third reticular axis
(not shown in the figure).

The
number of parts in which a family of planes cut the cell axes
can
be associated with a triplet of numbers that identify that
family
of planes. In the three previous figures, the number of cuts, and
therefore the numerical triplets would be (110), (210) and (310),
respectively, according to the vertical, horizontal and
perpendicular-to-the-figure axes. In this figure, the numerical
triplets for the planes drawn are (022), that
is, the family of planes does not cut the a
axis, but cuts the b
and c
axes in 2
identical parts, respectively.
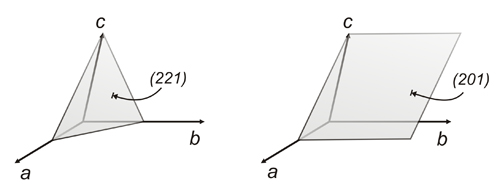
The plane drawn on the left side
of the figure
above cuts
the a
axis in 2
equal parts, the b
axis in 2
parts and the c
axis in 1
part. Hence, the numerical triplet identifying the plane will
be (221).
The plane drawn on the right side of the figure cuts the a
axis into 2
parts, is parallel to the b
axis and cuts the c
axis in 1
part. Therefore, the numerical triplet will be (201).
A unique plane, as the one drawn in
the top right figure, defined by the numerical
triplet known as Miller
indices,
represents and describes the whole family of parallel planes passing
through every element of the motif. Thus, in a crystal structure, there
will be as many plane families as possible numerical triplets
exist with the condition that these numbers are primes,
one to each other (not having a common divisor).
The Miller indices are
generically represented by the triplet of letters hkl.
If
there are common divisors among the Miller indices, the
numerical triplet
would represent a single family of planes only. For example, the family
with indices (330),
which are not strictly reticular, can be regarded as the representative
of 3
families of indices (110) with
a geometric
out-of-phase distance (among the families) of 1/3
of the
original (see the figures below).
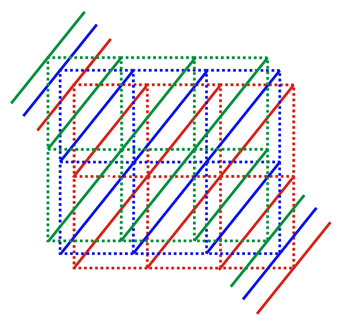
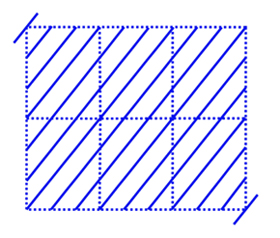
Left:
Three families
of reticular
planes, with indices (110)
in three equivalent lattices, showing an out-of-phase distance between
them of 1/3
of the interplanar spacing in each family.
Right:
The
same
set of planes of the figure on
the left drawn over one of the equivalent lattices. Therefore its
Miller indices are (330)
and its interplanar spacing is 1/3 of the
interplanar
spacing of the (110)
family.

Through
a point in the crystal (in the example in the center of the cell) we
can draw an infinite number of plane families with an infinite number
of
orientations. In this case only 3 families and 3 orientations are
shown.
Of
course, interplanar
spacings can be directly calculated from the Miller indices (hkl)
and the values of the reticular parameters (unit cell axes).
The
table below shows that these relations can be simplified for the
corresponding metric of the different lattices.

Formula to calculate the interplanar
spacings (dhkl)
for a family of planes with Miller indices hkl
in a unit cell of parameters a,
b,
c, α, β,
γ. In
the trigonal case a=b=c=A; α=β=γ.
In all cases, obviously, the
calculated interplanar spacing also
represents the distance between the cell origin and the nearest plane
of the family.
Interested readers should also have a look into the chapter on lattice
planes and Miller indices offered by the University of
Cambridge.
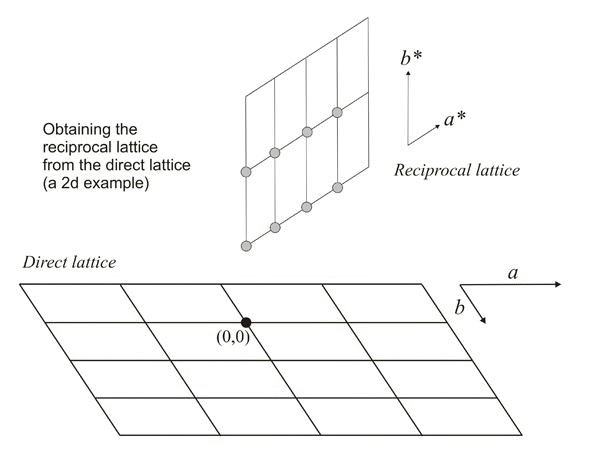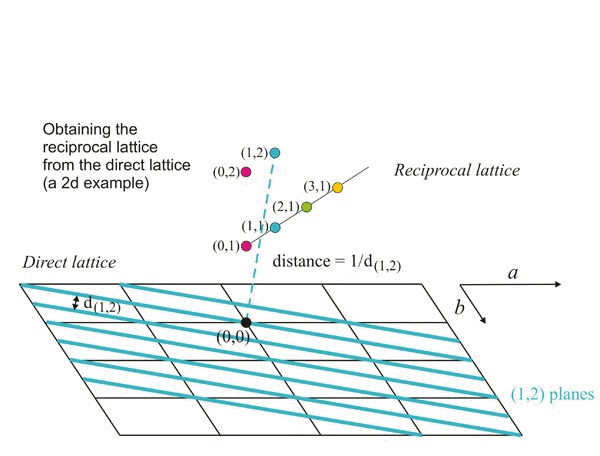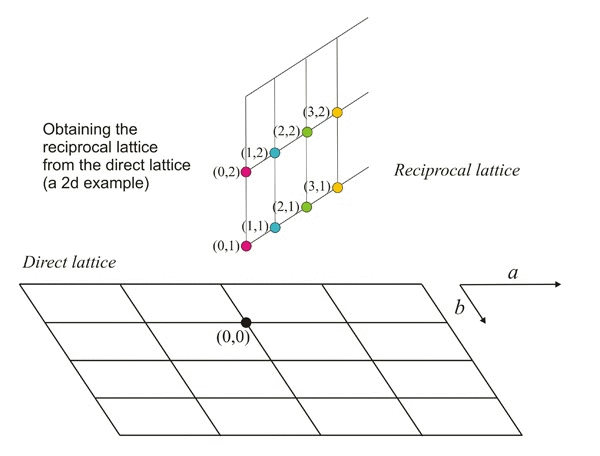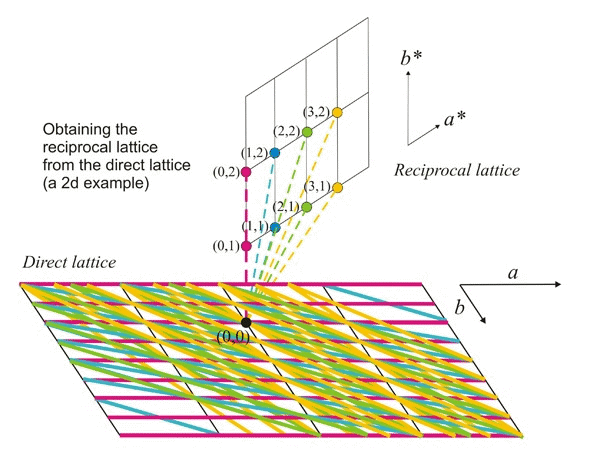
And now some more concepts
on lattices: the so called reciprocal lattice
...
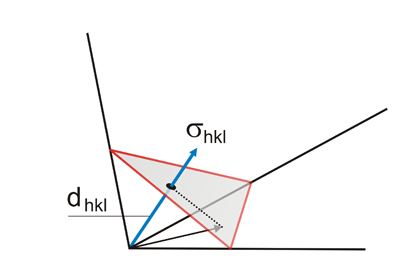
Any plane can also be
characterized by a vector (σhkl)
perpendicular to it. Therefore, the projection of the position
vector of any point (belonging to the plane), over
that
perpendicular line is constant and independent of the point.
It is
the distance of the plane to the origin, ie, the spacing (dhkl).
Any
plane can be represented by a vector
perpendicular to it.
Consider the family of
planes hkl
with the interplanar distance dhkl.
From the set of vectors normal to the planes' family, we take
the one (σhkl)
with length 1/dhkl.
The scalar product between this vector and the position vector (d'hkl
) of a point belonging to a plane from the family is an integer (n),
and this integer gives us the order of that plane in the hkl
family. That is:
(σhkl) . (d'hkl)
=
(1/dhkl) . (n.dhkl)
=
n
(see figure below)
n
will
be
0 for the
plane passing through the origin, 1
for the first plane, 2
for the second, etc.
Thus, σhkl
represents the whole family of hkl
planes having an interplanar spacing given by dhkl.
In particular, for the first plane we get: |σhkl|
dhkl
=
1.
If we
define 1/dhkl,
as the length of the vector σhkl,
the product of this vector, times the dhkl
spacing of the planes family is the
unit.
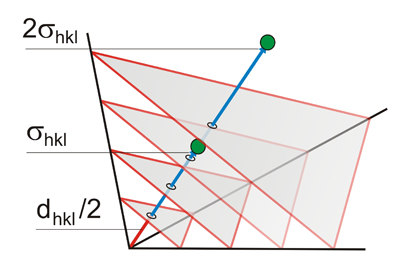
If we take a vector 2 times longer
than σhkl, the interplanar spacing of the
corresponding new family of planes would be a half.
If from this normal vector σhkl
of length 1/dhkl, we
take another vector, n times
(integer) longer (n.σhkl), the
above mentioned product (|σhkl|
dhkl
=
1)
would imply that the new vector (n.σhkl) will correspond
to a family of planes of indices nh,nk,nl
having an interplanar spacing n
times smaller. In other words, for instance, the lengths of the
following interplanar spacings will bear the relation: d100
= 2.(d200)=
3.(d
300)..., so that σ100 = (1/2).σ200 = (1/3).σ300 ... and similarly for
other hkl
planes.
Therefore, it appears that the
moduli (lengths) of the perpendicular vectors (σhkl)
are reciprocal
to the interplanar spacings.
The end points of these vectors (blue arrows in figure below) also
produce a periodic
lattice
that, due to this reciprocal property, is known as the reciprocal
lattice of the original direct lattice. The reciprocal
points obtained in this way (green points in figure below) are identified with the same
numerical triplets hkl
(Miller
indices) which
represent the corresponding plane family.

Geometrical
construction of some points of a reciprocal lattice (green
points)
from a direct lattice. To simplify, we assume that the third axis of
the
direct lattice (c)
is
perpendicular to the screen. The red lines represent the reticular
planes (perpendicular to the screen) and whose Miller indices are shown
in blue. As an example: the reciprocal point with
indices (3,1,0)
will be located on a vector
perpendicular to the plane (3,1,0)
and its distance to the origin O
is inversely proportional to the spacing
of that family of planes.
Animated example showing how to obtain
the reciprocal points from a direct lattice
It should now be clear that
the
direct lattice, and its reticular planes, are directly associated
(linked) with the reciprocal
lattice. Moreover, in this reciprocal lattice we can also
define a unit cell
(reciprocal
unit cell) whose periodic translations will be determined
by three reciprocal
axes that form reciprocal
angles among them. If the unit cell axes and
angles
of the direct cell are known by the letters a,
b,
c, α, β, γ,
the corresponding parameters for the reciprocal cell are written with
the same symbols, adding an asterisk: a*,
b*,
c*, α*, β*, γ*. It should also be clear that these
reciprocal axes (a*,
b*,
c*) will correspond to the
vectors σ100, σ010
and σ001, respectively, so that any reciprocal
vector can be expressed as a linear combination of these three reciprocal vectors:
σhkl
= h
a* + k b*
+ l
c*
Position vector of any reciprocal
point

Geometrical
relation between direct and reciprocal unit cells
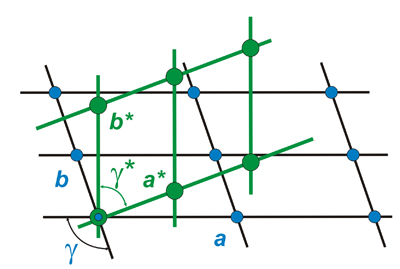
The
figure below shows
again the strong relationship between the two lattices (direct
with blue points, reciprocal
in green). In this case, the corresponding third
reciprocal axes (c
and c*)
are perpendicular to the screen.
And analytically the
relationship between the
direct (= real) and reciprocal cells can be written as:
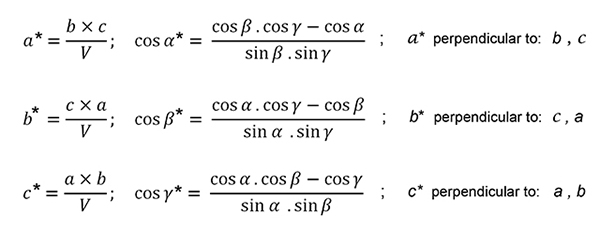
Metrical
relations among the parameters
defining the direct and reciprocal cells. V
represents
the volume of the direct cell and the symbol x
means
the cross product between two vectors.
The same type of equations can be written by changing the asterisks to
the right side of the equations. The volume of the direct
cell
can be calculated as:
V
= (a x b) . c = a. b. c (1 - cos2α -
cos2β -
cos2γ + 2 cos α
cos β cos γ)1/2
Note that, in accordance with
the definitions given above, the length of a*
is the inverse of the interplanar spacing d100
(|a*|
= 1/d100),
and that |b*|
= 1/d010,
and that |c*|
=
1/d001.
Therefore, the following scalar products (dot products) can be
written: a.a*
= 1,
a.b*
= 0 and
similarly with the other pairs of axes.
Summarizing:
- Direct space (= real
space) is the space
where we live..., where atoms are..., where crystals growth..., where
we imagine the direct lattices (= real lattices).
- Reciprocal space is a
mathematical
space constructed on the direct space (= real space). It is the space
where reciprocal lattices are, which will help us to
understand the crystal diffraction phenomena.
- “Big in direct space (that is, in
real
space)”, means “small in reciprocal
space”.
- “Small in direct space (that
is, in real
space)” means “big in reciprocal space”.
In
addition to this, we recommend to download and execute the Java
applet by Nicolas
Schoeni and Gervais Chapuis of the
Ecole Polytechnique
Fédéral de Lausanne (Switzerland) to understand the
relation between direct and reciprocal lattices and how to build the
latter from a direct lattice. (Free of any kind of virus).
See
also the pages on reciprocal
space offered by the University
of Cambridge through this link.
And
although we are
revealing aspects corresponding to the next chapter (see the last
paragraph of this page), the reader should also look at
the video made by www.PhysicsReimagined.com,
showing the geometric relationships between direct and reciprocal
lattices, displayed below as an animated gif:
The
reader is probably asking himself why we need this new concept (the
reciprocal
lattice). Well, there are reasons which justify it. One of
them is that a
family of planes
can be represented by
just one point,
which obviously simplifies things. And another important reason is
that this new lattice offer us a very simple geometric model
that can interpret the diffraction
phenomena in crystals. But
this will be described in another
chapter. Go on!
Next chapter: Scattering
and diffraction
Table of
contents